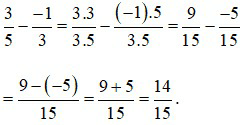Tìm số đối của các phân số sau:
 Giải bởi Vietjack
Giải bởi Vietjack
+) Số đối của phân số là
+) Số đối của phân số là hay hay
+) Số đối của phân số là
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Chị Chi mới đi làm và nhận được tháng lương đầu tiên. Chị quyết định dùng số tiền đó để chi tiêu trong tháng, dành số tiền để mua quà biếu bố mẹ. Tìm số phần tiền lương còn lại của chị Chi.
Mai tự nhẩm tính về thời gian biểu của mình trong một ngày thì thấy: thời gian là dành cho việc học ở trường; thời gian là dành cho các hoạt động ngoại khoá; thời gian dành cho hoạt động ăn, ngủ. Còn lại là thời gian dành cho các công việc cá nhân khác. Hỏi:
a) Mai đã dành bao nhiêu phần thời gian trong ngày cho việc học ở trường và hoạt động ngoại khoá?
b) Mai đã dành bao nhiêu phần thời gian trong ngày cho các công việc cá nhân khác?
Em hãy nhắc lại quy tắc cộng hai phân số cùng mẫu (có tử và mẫu dương) rồi tính các tổng: và
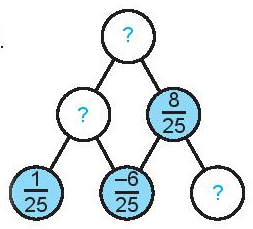
Thay dấu “?” bằng các phân số thích hợp để hoàn thiện sơ đồ bên, biết số trong mỗi ô ở hàng trên bằng tổng của hai số kề nó trong hai ô ở hàng dưới
Để thực hiện phép cộng , em hãy làm theo các bước sau:
- Quy đồng mẫu hai phân số và .
- Sử dụng quy tắc cộng hai phân số cùng mẫu để tính tổng hai phân số sau khi đã quy đồng.
Em hãy nhắc lại quy tắc trừ hai phân số (cả tử và mẫu đều dương) đã học rồi tính các hiệu sau: và
1. Phép cộng hai phân số
a) Cộng hai phân số cùng mẫu
– Muốn cộng hai phân số cùng mẫu, ta cộng các tử và giữ nguyên mẫu: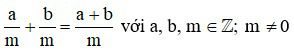
Ví dụ 1:
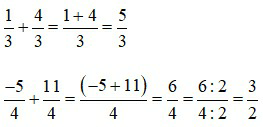
b) Cộng hai phân số không cùng mẫu số
– Muốn cộng hai phân số không cùng mẫu, ta viết chúng dưới dạng hai phân số cùng mẫu rồi cộng các tử và giữ nguyên mẫu.
Ví dụ 2:
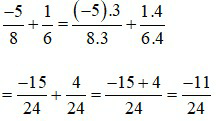
c) Số đối
– Hai số được gọi là đối nhau nếu tổng của chúng bằng 0. Kí hiệu số đối của phân số 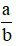 là
là 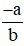 .
.

Ví dụ 3: 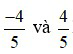 là hai phân số đối nhau vì
là hai phân số đối nhau vì 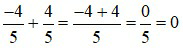
2. Tính chất của phép cộng hai phân số
Cho hai phân số 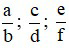 với a, b, c, d, e, f ∈ ℤ; b ≠ 0; d ≠ 0, f ≠ 0. Ta có:
với a, b, c, d, e, f ∈ ℤ; b ≠ 0; d ≠ 0, f ≠ 0. Ta có:
+ Tính chất giao hoán: 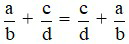
+ Tính chất kết hợp: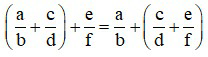
+ Tính chất cộng với số 0: 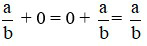
3. Phép trừ hai phân số
a) Trừ hai phân số cùng mẫu
– Muốn trừ hai phân số cùng mẫu, ta lấy tử số của phân số thứ nhất trừ đi tử số của phân số thứ hai và giữ nguyên mẫu số.
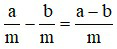 với a, b, m ∈ ℤ ; m ≠ 0.
với a, b, m ∈ ℤ ; m ≠ 0.
Ví dụ 4:
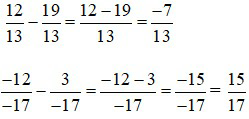
b) Trừ hai phân số không cùng mẫu:
– Muốn trừ hai phân số không cùng mẫu, ta quy đồng mẫu hai phân số rồi trừ hai phân số đó.
Ví dụ 5: