Báo Cheetah (Tri – tơ, H.6.2) được coi là động vật chạy nhanh nhất trên Trái Đất, tốc độ chạy có thể lên tới 120km/h (Theo vast.gov.vn). Mặc dù được mệnh danh là “chúa tể rừng xanh” nhưng tốc độ chạy tối đa của sư tử chỉ bằng khoảng tốc độ chạy tối đa của báo Cheetah. Tốc độ chạy tối đa của sư tử là bao nhiêu?
 Giải bởi Vietjack
Giải bởi Vietjack
Tốc độ chạy tối đa của sư tử bằng khoảng tốc độ chạy tối đa của báo Cheetah. Nghĩa là ta phải đi tìm của 120.
Do đó ta sẽ chia 120 thành 3 phần và lấy 2 phần trong 3 phần đó.
Khi đó, ta có:
Vậy tốc độ chạy tối đa của sư tử là 80km/h.
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Trong ngày thứ Sáu siêu khuyến mại hằng năm (Black Friday), 3/4 số mặt hàng trong một siêu thị được giảm giá. Tính ra có khoảng 6 000 mặt hàng được giảm giá trong ngày này. Hãy cho biết siêu thị có khoảng bao nhiêu mặt hàng.

Tàu ngầm lớp Kilo 636 trang bị cho Hải quân Việt Nam có thể lặn sâu tối đa tới 300 m.
(Theo vnexpress. net)
Để thực hiện một nhiệm vụ, tàu cần lặn tới độ sâu bằng 2/5 độ sâu tối đa. Em hãy tính xem khi đó tàu cách mực nước biển bao nhiêu mét.
1. Tìm giá trị phân số của một số cho trước
Muốn tìm 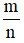 của một số a cho trước ta tính
của một số a cho trước ta tính 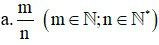
Ví dụ 1: 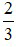 của 30 là
của 30 là 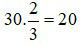
2. Tìm một số khi biết giá trị phân số của nó
– Muốn tìm một số biết 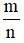 của số đó bằng b, ta tính
của số đó bằng b, ta tính 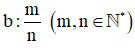
Ví dụ 2: Một người đi ra chợ để mua vải, người đó mua 25m vải ứng với 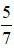 cuộn vải. Hỏi cuộn vải ban đầu dài bao nhiêu m.
cuộn vải. Hỏi cuộn vải ban đầu dài bao nhiêu m.
Lời giải:
Độ dài cuộn vải ban đầu là:
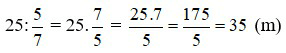
Vậy cuộn vải ban đầu dài 35m.