Mức tiêu thụ nhiên liệu của một chiếc xe máy là 1,6 lít trên 100 kilômét. Giá một lít xăng E5 RON 92-ll ngày 20-10-2020 là 14 260 đồng (đã bao gồm thuế). Một người đi chiếc xe máy đó trên quãng đường 100 km thì sẽ hết bao nhiêu tiền xăng?
 Giải bởi Vietjack
Giải bởi Vietjack
Số tiền xăng của người đi xe máy trên quãng đường 100km là:
14 260. 1,6 = 22 816 (đồng)
Vậy người đó đi quãng đường 100km hết 22 816 đồng tiền xăng.
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Tính giá trị của biểu thức sau:
21. 0,1 - [4 - (- 3,2 - 4,8)]: 0,1.
Điểm đông đặc và điểm sôi của thuỷ ngân lần lượt là - 38,83°C và 356,73°C. Một lượng thuỷ ngân đang để trong tủ bảo quản ở nhiệt độ - 51,2°C.
a) Ở nhiệt độ đó, thuỷ ngân ở thể rắn, thể lỏng hay thể khí?
b) Nhiệt độ của tủ phải tăng thêm bao nhiêu độ để lượng thuỷ ngân đó bắt đầu bay hơi?
Để nhân (chia) một số thập phân với 0,1; 0,01; 0,001;... ta chỉ cần dịch dấu phẩy của số thập phân đó sang trái (phải) 1, 2, 3... hàng, chẳng hạn:
2,057. 0,1 = 0,2057
-31,025: 0,01 = -3 102,5.
Tính nhẩm:
a) (- 4,125). 0,01;
b) (- 28,45): (- 0,01).
Từ độ cao - 0,21 km (so với mực nước biển), tàu thăm dò đáy biển bắt đầu lặn xuống. Biết rằng cứ sau mỗi phút, tàu lặn xuống sâu thêm được 0,021 km. Tính độ cao xác định vị trí tàu (so với mực nước biển) sau 10 phút kể từ khi tàu bắt đầu lặn.
Tính giá trị của các biểu thức sau:
a) 2,5. (4,1 – 3 - 2,5 + 2. 7,2) + 4,2: 2;
b) 2,86. 4 + 3,14. 4 - 6,01. 5 + .
Tài khoản vay ngân hàng của một chủ xưởng gỗ có số dư là -1,252 tỉ đồng. Sau khi chủ xưởng trả được một nửa khoản vay thì số dư trong tài khoản là bao nhiêu tỉ đồng?
Năm 2018, ngành giấy Việt Nam sản xuất được 3,674 triệu tấn. Biết rằng để sản xuất ra 1 tấn giấy phải dùng hết 4,4 tấn gỗ. Em hãy tính xem năm 2018 Việt Nam đã phải dùng bao nhiêu tấn gỗ cho sản xuất giấy.
(Theo vppa.vn)
Tính:
a) 8,625. (- 9);
b) (- 0,325). (- 2,35);
c) (- 9,5875): 2,95.
Tính:
a) (-12, 245) + (-8, 235);
b) (- 8, 451) + 9, 79
c) (-11, 254) - (-7, 35).
Một khối nước đá có nhiệt độ -4,5°C. Nhiệt độ của khối nước đá đó phải tăng thêm bao nhiêu độ để chuyển thành thể lỏng? (Biết điểm nóng chảy của nước đá là 0 °C)
Một tàu thăm dò đáy biển đang ở độ cao – 0,32 km (so với mực nước biển).
Tính độ cao mới của tàu (so với mực nước biển) sau khi tàu nổi lên thêm 0,11 km.
1. Phép cộng, trừ số thập phân
– Muốn cộng hai số thập phân âm, ta cộng hai số đối của của chúng và đặt dấu trừ đằng trước.
(–a) + (–b) = – (a + b) với a, b > 0
– Muốn cộng hai số thập phân khác dấu ta làm như sau:
+ Nếu 0 < a b thì (–a) + b = b – a
+ Nếu a > b > 0 thì (–a) + b = –(a – b)
– Tương tự với phép cộng của số nguyên và phép cộng của phân số, phép cộng hai số thập phân cũng có các tính chất giao hoán, tính chất kết hợp, tính chất cộng với số 0.
Cho a, b, c là ba số thập phân khi đó ta có:
Tính chất giao hoán: a + b = b + a
Tính chất kết hợp: (a + b) + c = a + (b + c)
Tính chất cộng với số 0: a + 0 = 0 + a = a.
– Phép trừ hai số thập phân được đưa về phép cộng hai số đối:
a – b = a + (–b)
Ví dụ 1:
a) 3, 17 + (–1, 12) = 3, 17 – 1, 12 = 2, 05
Trình bày theo cách đặt tính
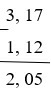
b) 4, 06 – 5, 13 = 4, 06 + (–5, 13) = –(5, 13 – 4, 06) = –1, 07
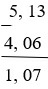
2. Phép nhân số thập phân
Ta thực hiện phép nhân hai số thập phân theo quy tắc tương tự như phép nhân hai số nguyên.
– Nhân hai số cùng dấu: (–a).(–b) = a.b với a, b > 0
– Nhân hai số khác dấu: (–a).b = a.(–b) = – (a.b) với a, b > 0
– Tương tự với phép nhân số nguyên và phép nhân phân số, phép nhân các số thập phân cũng có các tính chất giao hoán, tính chất kết hợp, tính chất nhân với 1, tính chất phân phối của phép cộng và phép nhân.
Cho ba số thập phân a, b, c ta có:
– Tính chất giao hoán: a.b = b.a
– Tính chất kết hợp: (a.b).c = a.(b.c)
– Tính chất nhân với số 1: a.1 = 1. a = a
– Tính chất phân phối giữa phép cộng và phép nhân: (a + b).c = a.c + b.c
Ví dụ 2:
(–2, 14) . (–3, 12) = 2, 14 . 3, 12 = 6, 6768
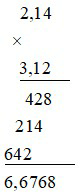
3. Phép chia số thập phân
Ta thực hiện phép chia hai số thập phân theo quy tắc tương tự như phép chia hai số nguyên.
– Chia hai số nguyên cùng dấu:
(–a) : (–b) = a : b với a, b > 0
– Chia hai số nguyên khác dấu:
(–a) : b = a : (–b) = –(a:b) với a, b > 0
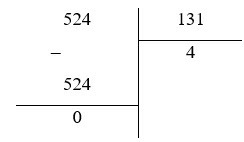
Ví dụ 3:
a) (–5, 24) : 1, 31 = –(5, 24 : 1, 31) = –(524 : 131) = –4
b) 24, 25 : (–0, 625) = –(24, 250 : 0, 625) = –(24 250 : 625) = –38,8
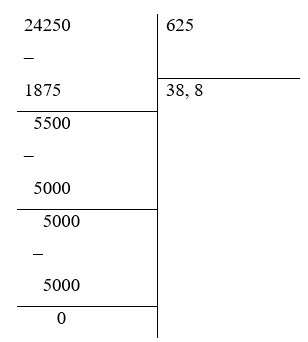
4. Tính giá trị biểu thức với số thập phân
Phép cộng và phép nhân số thập phân cũng có các tính chất giao hoán, kết hợp, phân phối như phép cộng, phép nhân số nguyên và phân số. Vận dụng các tính chất này và quy tắc dấu ngoặc, ta có thể tính giá trị biểu thức một cách hợp lí.
Ví dụ 4:
a) 12, 53 + 3, 47 – 2, 53 + 6, 53
= (12, 53 – 2, 53) + (3, 47 + 6, 53)
= 10 + 10 = 20
b) 35, 17 . 64, 25 + 35, 17 . 35, 75 – 2, 14 . 100
= 35, 17. (64, 25 + 35, 75) – 2, 14 . 100
= 35, 17. 100 – 2, 14 . 100
= 100 . (35, 17 – 2, 14)
= 100 . 33, 03 = 3303