Em có biết vì sao trong phần mở đầu đoạn tin bên, người ta lại viết "trên 232 triệu USD" thay vì viết "232,142 372 triệu USD"?

 Giải bởi Vietjack
Giải bởi Vietjack
Ta thấy trị giá 232, 142 372 triệu USD là con số nếu viết chính xác sẽ khá khó đọc và dài dòng, con số đó lớn hơn 232 nên để thuận tiện người ta viết “trên 232 triệu USD” thay vì “232, 142 372 triệu USD”.
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Chia đều một thanh gỗ dài 6,32 m thành bốn đoạn bằng nhau. Tính độ dài mỗi đoạn gỗ (làm tròn kết quả đến hàng phần mười).
a) Làm tròn 24,037 đến hàng phản mười ta được kết quả là 24,0.

Trong câu a, nếu viết kết quả làm tròn là 24 thì có đúng không?
Mẹ cho An 150 000 đồng để mua đồ dùng học tập. An dự định mua 15 quyền vở, 5 chiếc bút bi và 10 chiếc bút chì. Giá của một quyên vở, một chiếc bút bi, một chiếc bút chì lần lượt là 5 400 đồng, 2 800 đồng, 3 000 đồng. Em hãy ước lượng xem An có đủ tiền để mua đồ dùng học tập theo dự định không.
Để đo khoảng cách giữa các hành tinh trong Hệ Mặt Trời, người ta sử dụng đơn vị thiên văn là AU (1 AU xắp xỉ bằng khoảng cách giữa Trái Đất và Mặt Trời, được tính chính xác là 149 597 870 700 m). Để dễ viết, dễ nhớ, người ta nói 1 AU bằng khoảng 150 triệu kilômét.
Nói như vậy nghĩa là ta đã làm tròn số liệu trên đến hàng nào?
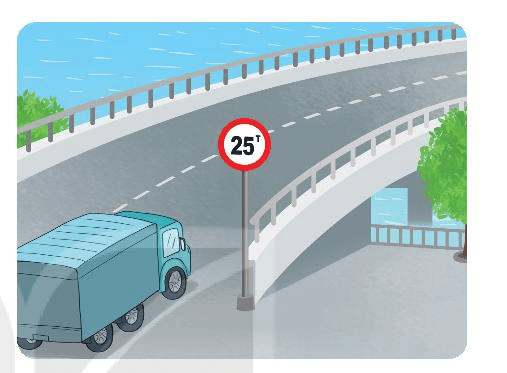
Một xe hàng có khối lượng khi không chở hàng hoá là 12 tấn. Trên xe chở 9 thùng hàng, mỗi thùng có khối lượng là 1,3 tấn. Một cây cầu có biển chỉ dẫn cho phép các xe có khối lượng không quá 25 tấn đi qua. Hỏi xe hàng trên có được phép qua cầu không?
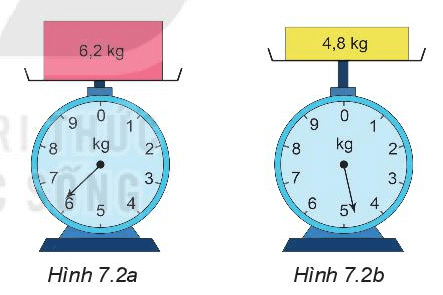
a) Theo em, khối lượng của hộp màu hồng nặng khoảng 6 kg hay 7 kg?
b) Khối lượng của hộp màu vàng nặng khoảng 4 kg hay 5 kg?
Em hãy đọc đoạn tin ngắn ở phần mở đầu rồi làm tròn số 479 633 đến hàng nghìn và làm tròn số 232,142 372 đến hàng đơn vị. So sánh hai kết quả với các số liệu trong tiêu đề của đoạn tin đó.

Trong bốn số sau có một số là kết quả của phép tính 256,3 + 892,37 + 45. Bằng cách ước lượng, em hãy cho biết số đó là số nào.
(A) 1 190,65
(B) 2 356,67
(C) 1 193,67
(D) 128,67
1. Làm tròn số
Để làm tròn một số thập phân dương đến một hàng nào đấy (gọi là hàng làm tròn), ta làm như sau:
– Đối với chữ số hàng làm tròn:
+ Giữ nguyên nếu chữ số ngay bên phải nhỏ hơn 5;
+ Tăng 1 đơn vị nếu chữ số ngay bên phải lớn hơn hay bằng 5.
– Đối với các chữ số sau hàng làm tròn:
+ Bỏ đi nếu ở phần thập phân
+ Thay bởi các chữ số 0 nếu ở phần số nguyên.
Ví dụ 1:
a) Làm tròn số 4, 12356 đến hàng phần trăm.
b) Làm tròn số 3124, 13 đến hàng trăm.
Lời giải:
a) Số 4, 12356
+ Bỏ đi các chữ số sau hàng phần trăm: bỏ đi 3; 5 và 6.
+ Vì số 3 bé hơn 5 nên chữ số 2 đứng trước nó giữ nguyên
Do đó làm tròn số 4, 12356 tới hàng phần trăm là 4, 12.
b) Số 3124, 13
+ Bỏ đi các chữ số sau hàng đơn vị là 1 và 3.
+ Thay các chữ số 2 và 4 bởi các số 0
+ Vì 2 < 5 nên chữ số hàng trăm là 1 được giữ nguyên
Làm tròn số 3124, 13 làm tròn đến hàng trăm ta được kết quả là 3100.
2. Ước lượng
Trong đời sống, đôi khi ta không quá quan tâm đến tính chính xác của kết quả mà chỉ cần ước lượng kết quả, tức là tìm một số gần sát với kết quả nhất. Để làm được việc ngày ta thường sẽ ước lượng các giá trị để có được kết quả ước lượng.
Có thể ước lượng kết quả bằng một trong các cách sau:
– Cắt bỏ bớt một hay nhiều chữ số ở phần thập phân của kết quả;
– Làm tròn kết quả tới một hàng thích hợp;
– Làm tròn các số hạng, thừa số, số bị chia, số chia có trong dãy phép tính cần thực hiện.
Ví dụ 2: Trong bốn số sau có một số là kết quả của phép tính 256, 3 + 892, 37 + 45. Bằng cách ước lượng, em hãy cho biết số đó là số nào.
(A) 1 190, 65
(B) 2 356, 67
(C) 1 193, 67
(D) 128, 67
Lời giải:
+) Làm tròn 256, 3 đến hàng đơn vị ta được kết quả là: 256
+) Làm tròn 892, 37 đến hàng đơn vị ta được kết quả là: 892
Do vậy tổng cần tính xấp xỉ bằng:
256 + 892 + 45 = (255 + 1) + 892 + 45 = (255 + 45) + (1 + 892)
= 300 + 893 = 1 193
Trong bốn đáp án, (B) và (D) quá xa với 1 193 nên loại (B), (D).
Ta thấy 1 193 gần (C) hơn nên khả năng (C) đúng.
Chú ý rằng tổng các chữ số hàng phần trăm là 7 nên (A) sai
Đáp án cần chọn: C