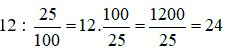Tính:
a) 25% của 8;
b) 7,5% của 180.
 Giải bởi Vietjack
Giải bởi Vietjack
a) 25% của 8 là:
b) 7,5% của 180 là:
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Theo Tổng cục Thống kê, năm 1989 cả nước có 914 396 người dân tộc Mường. Sau 30 năm số người Mường đã tăng lên thành 1 452 095 người. Em hãy cho biết trong 30 năm đó, số người Mường ở Việt Nam đã tăng bao nhiêu phần trăm (làm tròn kết quả đến hàng phần mười).
Giá niêm yết của một chiếc điện thoại di động là 625 nghìn đồng. Trong chương trình khuyến mại, mặt hàng này được giảm giá 10%. Như vậy, khi mua một chiếc điện thoại loại này người mua được giảm bao nhiêu tiền?
Trong một cuộc bình chọn cầu thủ xuất sắc nhất giải bóng đá của trường, Tân nhận được 120 phiếu bầu, chiếm 60% tổng số phiếu bình chọn. Hỏi có bao nhiêu người đã tham gia bình chọn?
Lãi suất tiền gửi kì hạn một năm của một ngân hàng là 7,4%. Bác Đức gửi 150 triệu đồng vào ngân hàng đó. Sau một năm, bác Đức rút cả vốn lẫn lãi thì nhận được bao nhiêu tiền?
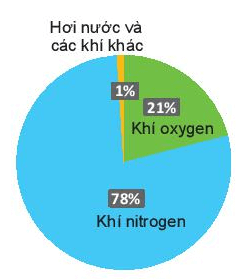
Không khí xung quanh ta gồm nhiều chất khí khác nhau. Trong điều kiện thông thường, khí oxygen chiếm khoảng 21% thể tích không khí. Hỏi có bao nhiêu mét khối oxygen trong một căn phòng có thể tích 70,2 ?
(Thành phần các chất trong không khí theo thể tích)
Trong đại hội chi đội lớp 6A, bạn Dũng được 36 đội viên (trong tổng số 45 đội viên chi đội) bầu làm Chi đội trưởng. Bạn Dũng đã trúng cử Chi đội trưởng với tỉ số phần trăm phiếu bầu là bao nhiêu?
Khoai lang là thực phẩm bổ dưỡng, giàu chất xơ và rất tốt cho sức khỏe. Theo Viện Dinh dưỡng Quốc gia, trong 200 gam khoai lang có chứa khoảng 57 gam chất bột đường và 2,6 gam chất xơ.
Viết tỉ số khối lượng chất bột đường và khối lượng của khoai lang.
Khoai lang là thực phẩm bổ dưỡng, giàu chất xơ và rất tốt cho sức khỏe. Theo Viện Dinh dưỡng Quốc gia, trong 200 gam khoai lang có chứa khoảng 57 gam chất bột đường và 2,6 gam chất xơ.
Bằng cách tương tự, em hãy viết tỉ số khối lượng chất xơ và khối lượng của khoai lang.
Viết tỉ số khối lượng chất xơ và khối lượng của khoai lang dưới dạng tỉ số phần trăm.
1. Tỉ số và tỉ số phần trăm
– Tỉ số của số a và số b là thương của phép chia a cho b, được viết là a : b (với b khác 0)
Tỉ số của hai đại lượng (cùng loại và cùng đơn vị đo) là tỉ số hai số đo cùng hai đại lượng đó.
Ví dụ 1:
Tỉ số của 3 và 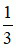 là 3 :
là 3 : 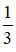
Tỉ số của 1 dm và 1 m là 1 : 10 vì ta phải đổi về cùng đơn vị do đó ta đổi 1 m = 10 dm.
– Trong thực hành, ta thường dùng tỉ số dưới dạng tỉ số phần trăm.
– Tỉ số phần trăm của hai số a và b là 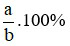
2. Hai bài toán về tỉ số phần trăm
Bài 1: Tìm giá trị phần trăm của một số cho trước.
Muốn tìm m % của một số a đã cho ta tính a .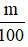
Ví dụ 2: 75% của 48 là 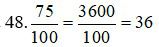
Bài 2: Tìm một số biết giá trị phần trăm của số đó:
Muốn tìm một số khi biết m % của số đó bằng b ta tính b :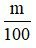
Ví dụ 3: 25 % của một số là 6 thì số đó là 6 : 25 % =