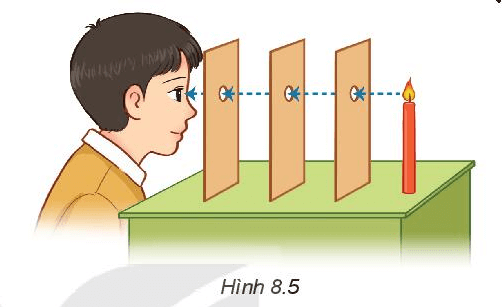
Một người nhìn qua các lỗ hổng được khoét trên các tấm bìa và thấy ngọn nến như Hình 8.5.
Em thấy các lỗ hổng có cùng nằm trên một đường thẳng không?
 Giải bởi Vietjack
Giải bởi Vietjack
Vì ánh sáng từ ngọn nến truyền đến mắt người theo đường thẳng, khi mắt người nhìn thấy ngọn nến thì ở giữa mắt và ngọn nến không có vật nào cản trở, do vậy các lỗ hổng phải cùng nằm trên một đường thẳng.
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Cho một đường thẳng d và hai điểm phân biệt A, B không thuộc d.
Tìm điểm C thuộc d sao cho A, B, C thẳng hàng. Khi nào không thể tìm được điểm C như vậy?
Cho bốn điểm A, B, C và D như hình vẽ sau.
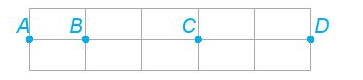
Hãy nêu tất cả các bộ ba điểm thẳng hàng.
Đánh dấu ba điểm phân biệt A, B và C trên một tờ giấy trắng sao cho chúng không thẳng hàng.
a) Hãy vẽ các đường thẳng đi qua hai trong ba điểm ấy. Đó là những đường thẳng nào?
b) Hãy chỉ ra hai đường thẳng cắt nhau và giao điểm của chúng.
Hãy tìm một số hình ảnh hai đường thẳng song song hay cắt nhau trong thực tế.
Quan sát Hình 8. 11.
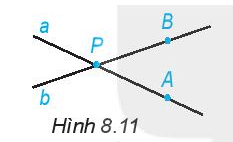
a) Giao điểm của hai đường thẳng a và b là điểm nào?
b) Điểm A thuộc đường thẳng nào và không thuộc đường thẳng nào? Hãy trả lời bằng câu diễn đạt và bằng kí hiệu.
Quan sát Hình 8. 12 và trả lời:
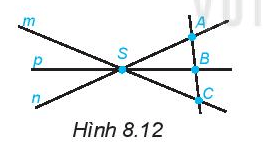
a) Có bao nhiêu bộ ba điểm thẳng hàng?
b) Hãy nêu ít nhất hai bộ ba điểm không thẳng hàng.
c) Bốn điểm A, B, C, S có thẳng hàng không?
Đánh dấu hai điểm phân biệt A, B trên một tờ giấy trắng.
- Dùng bút chì vẽ một đường thẳng đi qua hai điểm A, B.
- Tiếp tục dùng bút mực vẽ một đường thẳng đi qua hai điểm A, B
Em có nhận xét gì về hai đường thẳng vừa vẽ?
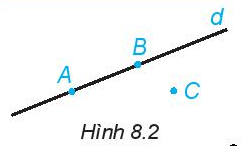
Trong Hình 8.2, những điểm nào thuộc đường thẳng d, điểm nào không thuộc đường thẳng d?
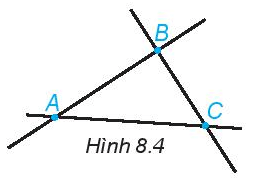
Hình 8.4 có bao nhiêu đường thẳng? Hãy đọc tên các đường thẳng đó.
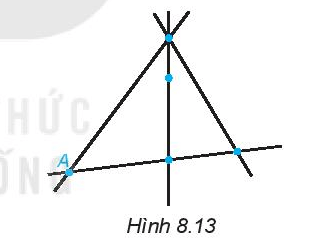
Hình 8.13 mô tả 4 đường thẳng và 5 điểm có tên là A, B, C, D và E, trong đó ta chỉ biết vị trí của điểm A. Hãy điền tên của các điểm còn lại, biết rằng:
(1) D nằm trên 3 trong 4 đường thẳng;
(2) Ba điểm A, B, C thẳng hàng;
(3) Ba điểm B, D, E thẳng hàng.
Trên sân vận động, người ta căng một sợi dây qua hai cái cọc được đóng ở hai vị trí đã chọn rồi dựa vào sợi dây đã căng để vẽ một vạch vôi. Em hãy giải thích tại sao người ta lại làm như vậy.
Hai đường thẳng phân biệt có thể có nhiều hơn một điểm chung được không?
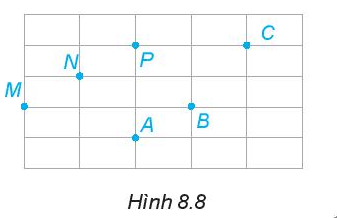
Em hãy dùng thước thẳng để kiểm tra trong Hình 8.8:
a) Ba điểm A, B, C có thẳng hàng không?
b) Ba điểm M, N, P có thẳng hàng không?
1. Điểm thuộc, không thuộc đường thẳng
a) Điểm, đường thẳng
- Dùng bút chấm 1 chấm nhỏ cho ta một hình ảnh về điểm.
- Dùng bút chì và thước thẳng, vẽ được một vạch thẳng cho ta hình ảnh về một đường thẳng.
- Ta thường dùng chữ cái in hoa để đặt tên điểm và dùng chữ cái thường để đặt tên đường thẳng.
Ví dụ 1:
- Điểm M; điểm N; điểm A; …
- Đường thẳng a; đường thẳng b; đường thẳng c; …
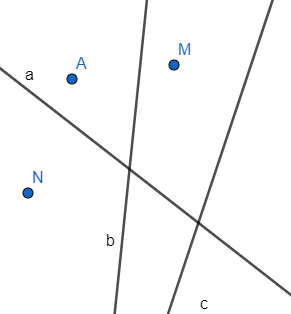
b) Điểm thuộc đường thẳng, điểm không thuộc đường thẳng
- Điểm thuộc đường thẳng nếu điểm đó nằm trên đường thẳng đó hay đường thẳng đó đi qua điểm đó.
- Điểm không thuộc đường thẳng nếu điểm đó không nằm trên đường thẳng hay đường thẳng đó không đi qua điểm đó.
- Ta dùng kí hiệu ∈ thể hiện điểm thuộc đường thẳng và ∉ để thể hiện điểm không thuộc đườn thẳng.
Ví dụ 2:
Quan sát hình vẽ ta có:
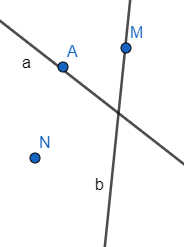
- Điểm A nằm trên đường thẳng a nên A ∈ a.
- Điểm M nằm trên đường thẳng b nên M ∈ b.
- Điểm A không nằm trên đường thẳng b nên A ∉ b.
- Điểm M không nằm trên đường thẳng a nên M ∉ a.
- Điểm N không nằm trên đường thẳng b nên N ∉ b.
- Điểm N không nằm trên đường thẳng a nên N ∉ a.
c) Đường thẳng đi qua hai điểm phân biệt
- Có một đường thẳng và chỉ một đường thẳng đi qua hai điểm phân biệt
Ví dụ 3: Qua hai điểm M, N ta chỉ vẽ được duy nhất một đường thẳng đi qua hai điểm M, N.

Chú ý: Để nhấn mạnh hai phía của đường thẳng, người ta còn dùng hai chữ cái thường để đặt tên, chẳng hạn đường thẳng xy (hoặc yx)

2. Ba điểm thẳng hàng
- Ba điểm thẳng hàng là ba điểm thuộc cùng một đường thẳng.
Ví dụ 4: Cho hai hình vẽ
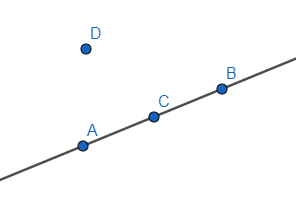
- Quan sát hình vẽ ta thấy
Ba điểm A, B, C thẳng hàng vì nó thuộc cùng một đường thẳng.
Ba điểm A, D, C không thẳng hàng vì nó không thuộc cùng một đường thẳng.
3. Hai đường thẳng song song, cắt nhau, trùng nhau.
- Hai đường thẳng song song là hai đường thẳng không có điểm chung. Kí hiệu song song là //.
- Hai đường thẳng cắt nhau là hai đường thẳng có một điểm chung.
- Hai đường thẳng trùng nhau là hai đường thẳng có vô số điểm chung.
|
|
|
|
|
a và b song song với nhau kí hiệu: a // b |
a và b cắt nhau tại điểm E |
Đường thẳng AB và đường thẳng BC trùng nhau. |