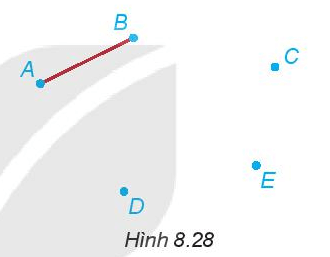
Có 5 hòn đảo biểu thị bởi 5 điểm A, B, C, D, E như Hình 8.28. Người ta đã xây một cây cầu nối hai đảo A và B (biểu thị bởi đoạn thẳng AB). Hỏi phải xây thêm ít nhất bao nhiêu cây cầu nữa để có thể đi lại giữa 5 hòn đảo đó qua những cây cầu (mỗi cây cầu chỉ nối hai đảo với nhau)?
 Giải bởi Vietjack
Giải bởi Vietjack
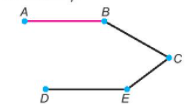
+) Bắt đầu từ A hoặc B mỗi lần muốn đi đến một hòn đảo mới, ta cần một cây cầu bắc đến hòn đảo đó, do vậy cần xây thêm ít nhất 3 cây cầu.
+) Dưới đây là một mô hình thể hiện:
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Nam dùng bước chân để đo chiều dài lớp học. Nam bước từ mép tường đầu lớp đến mép tường cuối lớp thì được đúng 18 bước chân. Nếu mỗi bước chân của Nam dài khoảng 0,6 m thì lớp học dài khoảng bao nhiêu mét?
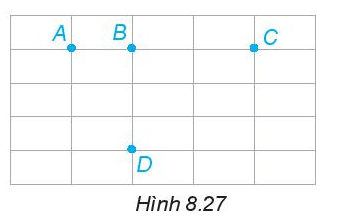
Với bốn điểm A, B, C, D như Hình 8.27, em hãy kể tên các đoạn thẳng có đầu mút là:
a) Hai trong ba điểm A, B, C;
b) Hai trong bốn điểm A, B, C, D.
Dùng thước thẳng có chia vạch, em hãy đo chiều dài của cây bút em đang dùng.
So sánh chiều dài cây bút với chiều dài thước thẳng và rút ra kết luận.
Một cái cây đang mọc thẳng thì bị bão làm gãy phần ngọn. Người ta đo được phần ngọn bị gãy dài 1,75 m và phần thân còn lại dài 3m. Hỏi trước khi bị gãy, cây cao bao nhiêu mét?
Một người đi xe đạp trên một đoạn đường thẳng từ A đến B (H.8.23).
Em có nhận xét gì về những vị trí mà người đó đã đi qua so với hai điểm A và B?

Lấy các điểm A, B, C, D phân biệt và thẳng hàng theo thứ tự như Hình 8.24.
Dùng thước thẳng và bút màu đen kẻ một vạch thẳng bắt đầu từ A và kết thúc ở B.
Em có nhận xét gì về vị trí của hai điểm C và D đối với phần vạch thẳng màu đen?

Việt dùng thước đo độ dài đoạn thẳng AB. Vì thước bị gãy mất một mẩu nên Việt chỉ có thể đặt thước để điểm A trùng với vạch 3 cm. Khi đó điểm B trùng với vạch 12 cm. Em hãy giúp Việt tính độ dài đoạn thẳng AB.
Dùng compa vẽ đường tròn tâm O có bán kính bằng 2 cm. Gọi M và N là hai điểm tuỳ ý trên đường tròn đó. Hai đoạn thẳng OM và ON có bằng nhau không?
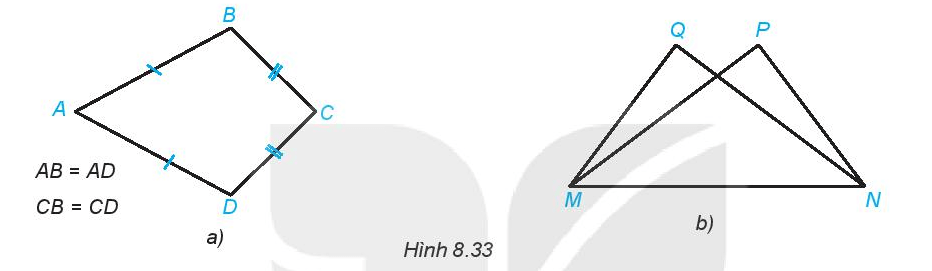
Em hãy đo các đoạn thẳng trong Hình 8.33b rồi đánh dấu giống nhau cho các đoạn thẳng bằng nhau theo mẫu như Hình 8.33a.
Mở trang cuối của sách giáo khoa, em sẽ thấy thông tin về khổ sách là 19 x 26,5 cm. Em hiểu thông tin đó như thế nào?
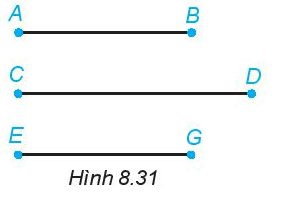
Dùng thước có vạch chia để đo độ dài các đoạn thẳng AB, CD, EG trong Hình 8.31 rồi trả lời các câu hỏi sau:
a) Đoạn thẳng AB có dài bằng đoạn thẳng EG không?
b) Trong các đoạn AB và CD, đoạn thẳng nào có độ dài nhỏ hơn?
c) Trong các đoạn CD và EG, đoạn thẳng nào có độ dài lớn hơn?
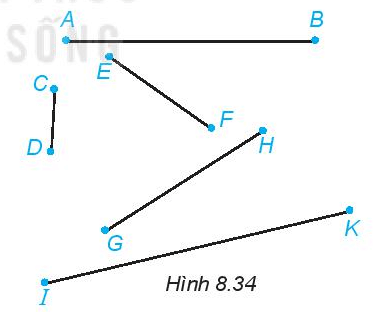
Hãy đo độ dài (đơn vị milimét) rồi sắp xếp các đoạn thẳng trong Hình 8.34 theo thứ tự tăng dần của độ dài.
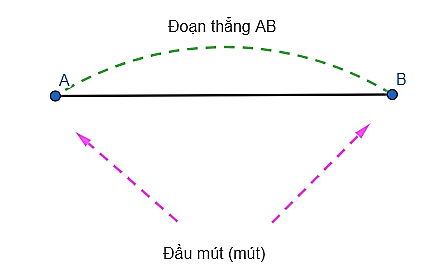
1. Đoạn thẳng
- Đoạn thẳng AB, hay đoạn thẳng BA, là hình gồm 2 điểm A, B cùng với tất cả các điểm nằm giữa A và B.
- A; B là hai đầu mút (mút) của đoạn thẳng AB.
Ví dụ 1: Đọc tên các đoạn thẳng có trong hình:
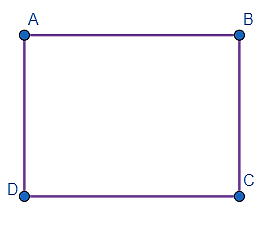
Các đoạn thẳng có trong hình là: AB; BC; CD; DA.
2. Độ dài đoạn thẳng
a) Độ dài đoạn thẳng
- Mỗi đoạn thẳng có một độ dài. Khi chọn một đơn vị độ dài thì độ dài mỗi đoạn thẳng được biểu diễn bởi một số dương (thường viết kèm đơn vị).
- Độ dài đoạn thẳng AB còn gọi là khoảng cách giữa hai điểm A và B. Ta quy ước khoảng cách giữa hai điểm trùng nhau bằng 0 (đơn vị).
- Đơn vị đo độ dài đoạn thẳng: mm; cm; dm; m; km…
Ví dụ 2: Quan sát hình vẽ
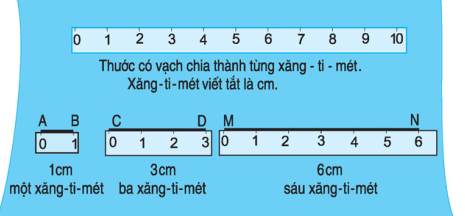
Ta thấy:
+ Độ dài đoạn thẳng AB là 1cm.
+ Độ dài đoạn thẳng CD là 3cm.
+ Độ dài đoạn thẳng MN là 6cm.
b) So sánh độ dài đoạn thẳng
- Hai đoạn thẳng AB và EG có cùng độ dài. Ta viết AB = EG và nói đoạn thẳng AB bằng đoạn thẳng EG.

- Đoạn thẳng AB có độ dài nhỏ nhơn đoạn thẳng CD. Ta viết AB < CD và nói AB ngắn hơn CD hoặc CD > AB và nói CD dài hơn AB.

c) Đo độ dài đoạn thẳng
Để đo độ dài đoạn thẳng ta làm như sau:
Bước 1: Đặt thước trùng với đường thẳng sao cho vạch 0 của thước trùng với một đầu mút của đoạn thẳng.
Bước 2: Quan sát xem đầu mút còn lại trùng với vạch mấy của thước thì số chỉ ở vạch đó chính là độ dài đoạn thẳng.
Chú ý: Nếu điểm M nằm giữa hai điểm A và B thì AM + MB = AB