Giả sử em có một cây gậy và muốn tìm điểm chính giữa của cây gậy đó. Em sẽ làm thế nào:
a) Dùng thước đo độ dài;
b) Chỉ dùng một sợi dây đủ dài.
 Giải bởi Vietjack
Giải bởi Vietjack
a) Dùng thước đo độ dài tìm điểm chính giữa của cây gậy ta làm như sau:
- Dùng thước đo độ dài của cây gậy.
- Lấy kết quả đo đó chia đôi, ta được khoảng cách từ trung điểm cây gậy đến các đầu mút của cây gậy.
- Dùng thước đo lại với khoảng cách vừa tìm được ta xác định được trung điểm của cây gậy.
b) Dùng sợi dây để tìm điểm chính giữa của cây gậy ta làm như sau:
- Ta đặt sợi dây sao cho thu được một đoạn bằng độ dài của cây gậy
- Ta gập đoạn sợi dây đó lại sao cho hai đầu sợi dây trùng nhau. Nếp gập cắt sợi dây thành hai phần bằng nhau.
Sau đó ta đặt sợi dây vừa gập lên cây gậy ta sẽ tìm được điểm chia cây gậy thành hai phần bằng nhau đó chính là trung điểm của cây gậy.
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Cho hình vẽ sau. Biết C là trung điểm của đoạn thẳng AB, D là trung điểm của đoạn thẳng AC. Biết rằng CD = 2 cm, hãy tính độ dài đoạn thẳng AB.

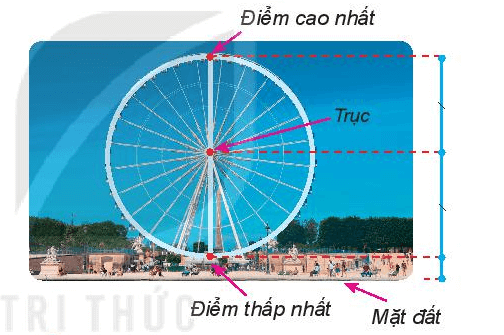
Vòng quay mặt trời trong một khu vui chơi có điểm cao nhất là 60 m, điểm thấp nhất là 6 m (so với mặt đất). Hỏi trục của vòng quay nằm ở độ cao nào?
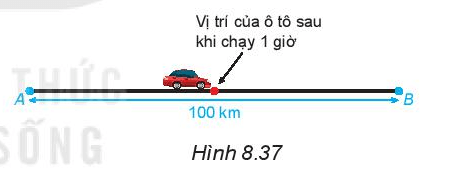
Một chiếc xe chạy với vận tốc không đổi trên một quãng đường thẳng dài 100 km từ vị trí A đến vị trí B hết 2 giờ.
Hỏi sau khi chạy được 1 giờ, xe rời xa vị trí A bao nhiêu kilômét, còn cách vị trí B bao nhiêu kilômét (H.8.37)?
Cho đoạn thẳng PQ dài 12 đơn vị. Gọi E là trung điểm của đoạn thẳng PQ và F là trung điểm của đoạn thẳng PE. Tính độ dài đoạn thẳng EF.

Người ta dùng một thanh gỗ dài 3 m để làm bập bênh. Theo em, điểm gắn trục phải cách hai đầu thanh gỗ là bao nhiêu?
Một sợi dây dài 120 cm. Gấp đôi sợi dây lại để hai đầu sợi dây trùng nhau. Đánh dấu điểm A là chỗ bị gập (H.8.36). Khoảng cách từ điểm A đến mỗi đầu sợi dây là bao nhiêu?

Cho hình vẽ sau:
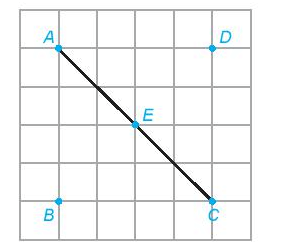
a) Em hãy dùng thước thẳng để kiểm tra xem điểm E có phải là trung điểm của đoạn AC không.
b) Kiểm tra xem E còn là trung điểm của đoạn thẳng nào khác có các đầu mút là các điểm đã cho.
Tính độ dài của đoạn thẳng AB nếu trung điểm I của đoạn thẳng AB nằm cách mút A một khoảng bằng 4,5 cm.
Dùng thước thẳng có vạch chia, em hãy kiểm tra xem các điểm I, J, K trong Hình 8.39 có lần lượt là trung điểm của các đoạn thẳng AB, CD, EF hay không.
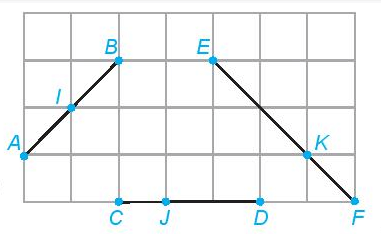
Hình 8.39
Em đã chơi bập bênh bao giờ chưa? Trong trò chơi này, người ta dùng một thanh gỗ dài gắn cố định trên một cái trục trên giá đỡ (H.8.35). Nếu hình dung thanh gỗ là một đoạn thẳng thì điểm đặt lên trục phải ở chính giữa đoạn thẳng đó.
Trong Hình học, điểm đó có ý nghĩa gì và làm thế nào để tìm nó?
- Nếu điểm I nằm giữa hai điểm A và B sao cho IA = IB thì I gọi là trung điểm của đoạn thẳng AB.
Khi đó:
IA = IB = 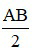 .
.
