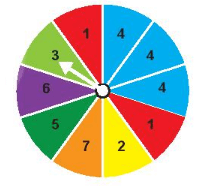
Minh quay tấm bìa và thấy mũi tên chỉ vào ô số 3 như hình bên.

Hãy cho biết sự kiện nào sau đây xảy ra:

(1) Mũi tên chỉ vào ô ghi số 3 hoặc 5.

(2) Mũi tên chỉ vào ô ghi số 4:

(3) Mũi tên chỉ vào ô ghi số lớn hơn 5. 

Gieo đồng thời 2 con xúc xắc. Quan sát số chấm xuất hiện và cho biết sự kiện nào sau đây xảy ra:

a) Tổng số chấm xuất hiện trên hai con xúc xắc là số chẵn;

b) Tổng số chấm xuất hiện trên hai con xúc xắc lớn hơn 7.

Quay tấm bìa như hình sau và xem mũi tên chỉ vào ô nào khi tấm bìa dừng lại.

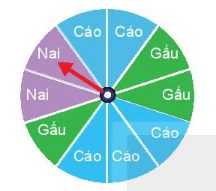
a) Liệt kê các kết quả có thể của thí nghiệm này;

b) Liệt kê các kết quả có thể để sự kiện Mũi tên không chỉ vào ô Nai xảy ra;

c) Nếu mũi tên chỉ vào ô Nai như hình vẽ thì sự kiện Mũi tên chỉ vào ô Gấu hoặc Nai có xảy ra không?

Gieo một con xúc xắc.

a) Liệt kê các kết quả có thể để sự kiện số chấm xuất hiện là số nguyên tố xảy ra;

b) Nếu số chấm xuất hiện là 5 thì sự kiện số chấm xuất hiện không phải là 6 có xảy ra hay không?

Một túi có 3 quả bóng màu đỏ và 3 quả bóng màu xanh có cùng kích thước

Không nhìn vào túi, lấy ra một quả bóng, ghi lại màu của quả bóng được lấy ra. Liệt kê các kết quả có thể xảy ra trong thí nghiệm này. 

Khi lấy bóng mà không nhìn vào túi ta nói bóng được chọn ngẫu nhiên.

Trò chơi dành cho hai người chơi. Mỗi người chơi chọn một trong sáu số 1, 2, 3, 4, 5, 6 rồi gieo con xúc xắc năm lần liên tiếp

Mỗi lần gieo, nếu xuất hiện mặt có số chấm bằng số đã chọn thì được 10 điểm, ngược lại bì trừ 5 điểm. Ai được nhiều điểm hơn sẽ thắng.

An và Bình cùng chơi. An chọn số 3 và Bình chọn số 4. Kết quả gieo của An và Bình lần lượt là 2, 3, 6, 4, 3 và 4, 3, 4, 5, 4. Hỏi An hay Bình là người thắng?

Vuông và Tròn gieo một con xúc xắc và quan sát mặt xuất hiện của nó. Có thể xảy ra những kết quả nào?

Chiếc nón kì diệu từng là một trò chơi truyền hình nổi tiếng ở Việt Nam .

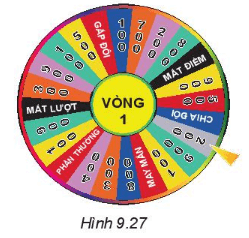
Quan sát Hình 9.27 và liệt kê tất cả các kết quả có thể khi quay chiếc nón kì diệu. 

a) Liệt kê các kết quả có thể về phần thưởng trong trò chơi Ô cửa bí mật.

b) Tìm một trò chơi, thí nghiệm khác và liệt kê các kết quả có thể của trò chơi, thí nghiệm đó.

Trong trò chơi Ô cửa bí mật, người ta đặt ba phần thưởng gồm một chiếc ô tô và hai con dê sau ba ô cửa. Người chơi sẽ chọn ngẫu nhiên một ô cửa và nhận được phần thưởng sau ô cửa đó. 

Mai và Linh cùng chơi, mỗi người gieo một đồng xu liên tiếp 30 lần được kết quả như sau ( S: sấp; N: ngửa)

Mai: S N N S S N S N S N S N N S S N N S S N N N S S S N N N S S .

Linh: N S S N N S N S N S S S S N S N N S S S N N N S S S N N S S.

Người chơi được một điểm khi có đúng ba lần liên tiếp đồng xu ra mặt ngửa. người nào được nhiều điểm hơn là người thắng.

Sự kiện Mai thắng có xảy ra hay không?

Một hộp kín đựng 5 viên bi xanh, 3 viên bi đỏ và 2 viên bi vàng có cùng kích thước. Mỗi lượt chơi, Minh và Khoa lần lượt lấy ra một viên bi từ hộp. Quan sát và ghi lại màu của viên bi rồi trả lại viên bi vào hộp.

Màu của các viên bi trong mỗi lượt lấy được Minh và Khoa ghi lại như hình bên (X: xanh, Ð: đỏ, V: vàng).

Người thắng là người lấy được nhiều viên bi đỏ hơn sau 10 lượt chơi. Sự kiện Minh thắng có xảy ra không?

Trong hộp có 10 tấm thẻ ghi các số 2; 2; 3; 3; 3; 5; 5; 5; 5; 5. Yêu cầu 5 bạn lần lượt rút ngẫu nhiên 1 thẻ, quan sát số ghi trên thẻ rồi trả lại thẻ vào hộp.

Sau mỗi lần một bạn rút, hãy cho biết các sự kiện sau có xảy ra hay không.

a) Rút được thẻ ghi số 5;

b) Không rút được thẻ ghi số 2.

Trong trò chơi ô cửa bí mật, người ta đặt ba phần thưởng gồm một chiếc ô tô và hai con dê sau ba ô cửa.

Người chơi sẽ chọn ngẫu nhiên một ô cửa và nhận phần thưởng sau ba ô cửa đó.

Liệu người chơi có may mắn nhận được phần thưởng là chiếc ô tô không?

Vuông và Tròn đang chơi trò oẳn-tù-tì. Em hãy liệt kê các kết quả Vuông có thể ra trong mỗi lần oẳn-tù-tì.

Em có đồng ý với Vuông không?