Chuẩn bị: Hai con xúc xắc xanh và đỏ.

Cách chơi: 

- Hai người chơi bốc thăm hoặc oẳn tù tì để chọn người chơi trước và mang tên E (Even number), người chơi sau mang tên O (Odd number). 

- Hai người chơi lần lượt gieo đồng thời hai con xúc xắc. Ở mỗi lần gieo, nếu tích số chấm xuât hiện trên hai con xúc xắc là số lẻ thì O được 1 điểm, là số chẵn thì E được 1 điểm. 

- Ai được 20 điểm trước là người thắng. 

1. Em đọc luật chơi trên và dự đoán xem trong hai người chơi, ai là người có khả năng thắng cuộc cao hơn.

2. Chia lớp thành từng cặp hai người chơi. Mỗi cặp chơi một ván (tức là chơi đến lúc có người thắng) và ghi lại kết quả theo mẫu Bảng 9.9.

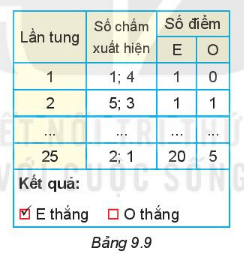
3. Tổng hợp lại kết quả chơi của cả lớp theo mẫu Bảng 9.10.

Cặp chơi số	E thắng	O thắng
1	X
2		X
…

Bảng 9.10

4. Từ dữ liệu Bảng 9.10, hãy tính xác suất thực nghiệm của các sự kiện E thắng, O thắng. Dựa vào kết quả tính được, khả năng E hay O thắng là cao hơn? Dự đoán ban đầu của em có chính xác không?

Nếu tung một đồng xu 22 lần liên tiếp thì, có 14 lần xuất hiện mặt N thì xác suất thực nghiệm xuất hiện mặt N bằng bao nhiêu?

Nếu tung một đồng xu 30 lần liên tiếp có 12 lần xuất hiện mặt N thì xác suất thực nghiệm xuất hiện mặt S bằng bao nhiêu?

Một hộp có 5 chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số 1, 2, 3, 4, 5; hai thẻ khác nhau thì ghi số khác nhau. Rút ngẫu nhiên một thẻ rồi bỏ lại thẻ vào hộp.

Sau 25 lần rút thẻ liên tiếp, hãy ghi kết quả thống kê theo mẫu sau:

Tính xác suất thực nghiệm

Xuất hiện số chẵn

Một hộp có 5 chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số 1, 2, 3, 4, 5; hai thẻ khác nhau thì ghi số khác nhau. Rút ngẫu nhiên một thẻ rồi bỏ lại thẻ vào hộp.

Sau 25 lần rút thẻ liên tiếp, hãy ghi kết quả thống kê theo mẫu sau:

Tính xác suất thực nghiệm

Xuất hiện số 2 

Một hộp có 5 chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số 1, 2, 3, 4, 5; hai thẻ khác nhau thì ghi số khác nhau. Rút ngẫu nhiên một thẻ rồi bỏ lại thẻ vào hộp.

Sau 25 lần rút thẻ liên tiếp, hãy ghi kết quả thống kê theo mẫu sau:

Tính xác suất thực nghiệm

Xuất hiện số 1

Trong hộp có 10 lá thư có bì thư giống nhau, bên trong mỗi bì thư có 1 lá thư và được đánh số từ 1 đến 10. Mỗi bạn lấy ngẫu nhiên một bì thư, xem số ghi trên lá thư rồi trả lại vào bì và cho vào hộp. Sự kiện có thể xảy ra là

Trong một hộp có 1 quả bóng xanh và 9 bóng vàng có kích thước giống nhau. An lấy ra đồng thời 2 bóng từ hộp. Có các sự kiện sau:

1- An lấy được 2 bóng màu xanh

2- An lấy được ít nhất một bóng màu vàng

3- An lấy được 2 bóng màu vàng.

Sự kiện chắc chắn, không thể và có thể xảy ra lần lượt là