Lớp 6A có 45 học sinh, có thể chia lớp thành hai nhóm, mỗi nhóm có số lượng học sinh bằng nhau.
A. Đúng
B. Sai
Giải bởi Vietjack
Trả lời:
Để mỗi nhóm có số lượng học sinh bằng nhau thì 45 phải chia hết cho 2.
Điều này không xảy ra vì chữ số tận cùng của 45 là 5 nên 45 không chia hết cho 2.
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Trong những số sau, có bao nhiêu số chia hết cho 5?
10005459, 12345, 1254360, 1234544, 155498
Bà Huệ có 19 quả xoài và 40 quả quýt. Khẳng định nào sau đây đúng?
Cho \[\overline {17*} \] chia hết cho 2. Số thay thế cho * có thể là
Tìm chữ số thích hợp ở dấu * để số \[\overline {212*} \] vừa chia hết cho 2 vừa chia hết cho 5.
Tìm các số tự nhiên x vừa chia hết cho 2 vừa chia hết cho 5 và 1998 < x < 2018.
Cô giáo có một số quyển vở đủ để chia đều cho 5 bạn điểm cao nhất lớp trong kì thi. Hỏi cô giáo có bao nhiêu quyển vở biết rằng cô giáo có số vở nhiều hơn 30 và ít hơn 40 quyển?
1. Dấu hiệu chia hết cho 2
Các số có chữ số tận cùng là 0; 2; 4; 6; 8 (tức là chữ số chẵn) thì chia hết cho 2 và chỉ những số đó mới chia hết cho 2.
Ví dụ:
a) Số 15 552 chia hết cho 2 vì có chữ số tận cùng là 2.
b) Số 955 không chia hết cho 2 vì có chữ số tận cùng là 5 (5 không là số chẵn).
2. Dấu hiệu chia hết cho 5
Các số có chữ số tận cùng là 0 hoặc 5 thì chia hết cho 5 và chỉ những số đó mới chia hết cho 5.
Ví dụ: Xét số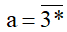 
. Thay * bởi số nào thì a chia hết cho 5, bởi số nào thì a không chia hết cho 5?
Hướng dẫn giải
Chữ số tận cùng của a là ∗ nên để a chia hết cho 5 thì ∗ phải là 0 hoặc 5.
Để a không chia hết cho 5 thì ∗ phải khác 0 hoặc 5, tức là các số 1; 2; 3; 4; 6; 7; 8; 9.
Vậy thay ∗ bằng 1; 2; 3; 4; 6; 7; 8; 9 thì a không chia hết cho 5.
Một hộp có 5 chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số 1, 2, 3, 4, 5; hai thẻ khác nhau thì ghi số khác nhau. Rút ngẫu nhiên một thẻ rồi bỏ lại thẻ vào hộp.
Sau 25 lần rút thẻ liên tiếp, hãy ghi kết quả thống kê theo mẫu sau:
|
Lần 1 |
Số 3 |
Lần 6 |
Số 5 |
Lần 11 |
Số 3 |
Lần 16 |
Số 2 |
Lần 21 |
Số 1 |
|
Lần 2 |
Số 1 |
Lần 7 |
Số 2 |
Lần 12 |
Số 2 |
Lần 17 |
Số 1 |
Lần 22 |
Số 5 |
|
Lần 3 |
Số 2 |
Lần 8 |
Số 3 |
Lần 13 |
Số 2 |
Lần 18 |
Số 2 |
Lần 23 |
Số 3 |
|
Lần 4 |
Số 3 |
Lần 9 |
Số 4 |
Lần 14 |
Số 1 |
Lần 19 |
Số 3 |
Lần 24 |
Số 4 |
|
Lần 5 |
Số 4 |
Lần 10 |
Số 5 |
Lần 15 |
Số 5 |
Lần 20 |
Số 5 |
Lần 25 |
Số 5 |
Tính xác suất thực nghiệm
Xuất hiện số chẵn
Một hộp có 5 chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số 1, 2, 3, 4, 5; hai thẻ khác nhau thì ghi số khác nhau. Rút ngẫu nhiên một thẻ rồi bỏ lại thẻ vào hộp.
Sau 25 lần rút thẻ liên tiếp, hãy ghi kết quả thống kê theo mẫu sau:
|
Lần 1 |
Số 3 |
Lần 6 |
Số 5 |
Lần 11 |
Số 3 |
Lần 16 |
Số 2 |
Lần 21 |
Số 1 |
|
Lần 2 |
Số 1 |
Lần 7 |
Số 2 |
Lần 12 |
Số 2 |
Lần 17 |
Số 1 |
Lần 22 |
Số 5 |
|
Lần 3 |
Số 2 |
Lần 8 |
Số 3 |
Lần 13 |
Số 2 |
Lần 18 |
Số 2 |
Lần 23 |
Số 3 |
|
Lần 4 |
Số 3 |
Lần 9 |
Số 4 |
Lần 14 |
Số 1 |
Lần 19 |
Số 3 |
Lần 24 |
Số 4 |
|
Lần 5 |
Số 4 |
Lần 10 |
Số 5 |
Lần 15 |
Số 5 |
Lần 20 |
Số 5 |
Lần 25 |
Số 5 |
Tính xác suất thực nghiệm
Xuất hiện số 2
Một hộp có 5 chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số 1, 2, 3, 4, 5; hai thẻ khác nhau thì ghi số khác nhau. Rút ngẫu nhiên một thẻ rồi bỏ lại thẻ vào hộp.
Sau 25 lần rút thẻ liên tiếp, hãy ghi kết quả thống kê theo mẫu sau:
|
Lần 1 |
Số 3 |
Lần 6 |
Số 5 |
Lần 11 |
Số 3 |
Lần 16 |
Số 2 |
Lần 21 |
Số 1 |
|
Lần 2 |
Số 1 |
Lần 7 |
Số 2 |
Lần 12 |
Số 2 |
Lần 17 |
Số 1 |
Lần 22 |
Số 5 |
|
Lần 3 |
Số 2 |
Lần 8 |
Số 3 |
Lần 13 |
Số 2 |
Lần 18 |
Số 2 |
Lần 23 |
Số 3 |
|
Lần 4 |
Số 3 |
Lần 9 |
Số 4 |
Lần 14 |
Số 1 |
Lần 19 |
Số 3 |
Lần 24 |
Số 4 |
|
Lần 5 |
Số 4 |
Lần 10 |
Số 5 |
Lần 15 |
Số 5 |
Lần 20 |
Số 5 |
Lần 25 |
Số 5 |
Tính xác suất thực nghiệm
Xuất hiện số 1
