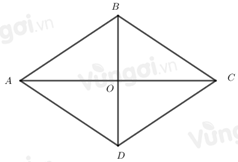
Cho hình thoi ABCD (AC >BD) có AC = 10cm, khẳng định nào sau đây đúng:

1. Hình chữ nhật

Hình chữ nhật có:

+ Bốn đỉnh.

+ Hai cặp cạnh đối diện bằng nhau.

+ Hai cặp cạnh đối diện song song.

+ Bốn góc ở các đỉnh bằng nhau và bằng góc vuông.

+ Hai đường chéo bằng nhau và cắt nhau tại trung điểm của mỗi đường.

Ví dụ:

Hình chữ nhật ABCD có:

- Bốn đỉnh A, B, C, D.

- Hai cặp cạnh đối diện bằng nhau: AB = CD; BC = AD.

- Hai cặp cạnh đối diện song song: AB song song với CD; BC song song với AD.

- Bốn góc ở đỉnh A, B, C, D bằng nhau và bằng góc vuông.

- Hai đường chéo bằng nhau và cắt nhau tại trung điểm của mỗi đường:

AC = BD và OA = OC; OB = OD.

Cách vẽ hình chữ nhật

Bước 1. Vẽ theo một cạnh góc vuông của ê ke đoạn thẳng AB có độ dài bằng 6 cm.

Bước 2. Đặt đỉnh góc vuông của ê ke trùng với điểm A và một cạnh ê ke nằm trên AB, vẽ theo cạnh kia của ê ke đoạn thẳng AD có độ dài bằng 9 cm.

Bước 3. Xoay ê ke rồi thực hiện tương tự như ở Bước 2 để được cạnh BC có độ dài bằng 9 cm.

Bước 4. Vẽ đoạn thẳng CD. Ta được hình chữ nhật ABCD.

2. Hình thoi

Hình thoi có:

+ Bốn đỉnh.

+ Bốn cạnh bằng nhau.

+ Hai cặp cạnh đối diện song song với nhau.

+ Hai đường chéo vuông góc với nhau.

Ví dụ:

Hình thoi ABCD có:

- Bốn đỉnh A, B, C, D.

- Bốn cạnh bằng nhau: AB = BC = CD = DA;

- Hai cạnh đối AB và CD, AD và BC song song với nhau.

- Hai đường chéo AC và BD vuông góc với nhau.

Cách vẽ hình thoi

Ví dụ: Dùng thước và compa vẽ hình thoi ABCD, biết AB = 5 cm và AC = 8 cm.

Hướng dẫn giải

Bước 1. Dùng thước vẽ đoạn thẳng AC = 8 cm.

Bước 2. Dùng compa vẽ một phần đường tròn tâm A bán kính 5 cm.

Bước 3. Dùng compa vẽ một phần đường tròn tâm C bán kính 5cm; phần đường tròn này cắt phần đường tròn tấm A vẽ ở Bước 2 tại các điểm B và D.

Bước 4. Dùng thước vẽ các đoạn thẳng AB, BC, CD, DA. Ta được hình thoi ABCD (như hình vẽ).

3. Hình bình hành

Hình bình hành có:

+ Bốn đỉnh.

+ Hai cặp cạnh đối diện bằng nhau.

+ Hai cặp cạnh đối diện song song.

+ Hai cặp góc đối diện bằng nhau.

+ Hai đường chéo cắt nhau tại trung điểm của mỗi đường.

Ví dụ:

Hình bình hành ABCD có:

- Bốn đỉnh A, B, C, D.

- Hai cặp cạnh đối diện bằng nhau: AB = CD; BC = AD.

- Hai cặp cạnh đối diện song song: AB song song với CD; BC song song với AD.

- Hai cặp góc đối diện bằng nhau: góc đỉnh A bằng góc đỉnh C; góc đỉnh B bằng góc đỉnh D.

- Hai đường chéo cắt nhau tại trung điểm của mỗi đường: OA = OC; OB = OD.

Cách vẽ hình bình hành

Hình bình hành ABCD có hai cạnh là a và b.

Bước 1: Vẽ đoạn thẳng AB = a (cm).

Bước 2: Vẽ đường thẳng đi qua B. Lấy điểm C trên đường thẳng đó sao cho BC = b (cm).

Bước 3: Vẽ đường thẳng đi qua A và song song với cạnh BC, đường thẳng qua C và song song với AB. Hai đường thẳng này cắt nhau tại D, ta được hình bình hành ABCD.

4. Hình thang cân

Hình thang cân có:

+ Hai cạnh đáy song song.

+ Hai cạnh bên bằng nhau.

+ Hai góc kề một đáy bằng nhau.

+ Hai đường chéo bằng nhau.

Ví dụ:

Hình thang cân EFGH có:

- Hai cạnh đáy song song: EF song song với GH.

- Hai cạnh bên bằng nhau: EH = FG.

- Hai góc kề một đáy bằng nhau: góc đỉnh E bằng góc đỉnh F, góc đỉnh G bằng góc đỉnh H.

- Hai đường chéo bằng nhau: EG = FH.

Cách gấp hình thang cân

Bước 1: Gấp đôi một tờ giấy hình chữ nhật.

Bước 2: Vẽ một đoạn thẳng nối hai điểm tùy ý trên hai cạnh đối diện (cạnh không chứa nếp gấp). Cắt theo đường nét đứt như hình minh họa.

Bước 3: Mở tờ giấy ra ta được một hình thang cân.