Cho các phân số \[\frac{6}{{n + 8}};\frac{7}{{n + 9}};\frac{8}{{n + 10}};...;\frac{{35}}{{n + 37}}\]. Tìm số tự nhiên n nhỏ nhất để các phân số trên tối giản.

1. Tính chất 1

Tính chất 1: Nếu nhân cả tử số và mẫu của một phân số với cùng một số nguyên khác 0 thì ta được một phân số mới bằng phân số đã cho.

Ví dụ 1. Cho phân số 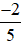. Nhân cả tử và mẫu của phân số  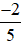với 3, ta được:

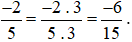
Khi đó, ta có phân số mới là 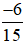 bằng phân số đã cho là .

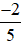Nhận xét: Có thể biểu diễn số nguyên ở dạng phân số với mẫu số (khác 0) tùy ý.

- Áp dụng tính chất 1, ta có thể quy đồng mẫu số hai phân số bằng cách nhân tử và mẫu mỗi phân số với số nguyên thích hợp.

Ví dụ 2. Có thể biểu diễn số −8 ở dạng phân số có mẫu số là 3 như sau:

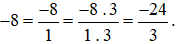
Ví dụ 3. Quy đồng mẫu số hai phân số .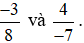

Lời giải: 

Quy đồng mẫu số hai phân số ta thực hiện như sau:

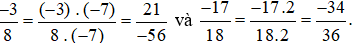
Nhận xét: Mẫu số giống nhau ở hai phân số là −56 còn gọi là mẫu số chung của hai phân số.

Khi quy đồng mẫu số hai phân số, có thể có nhiều cách chọn mẫu số chung.

Chú ý: Có thể quy đồng mẫu số của nhiều phân số bằng cách tìm mẫu số chung của nhiều phân số.

Ví dụ 4. Quy đồng mẫu số của ba phân số .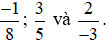

Lời giải: 

Quy đồng mẫu số ba phân số, ta nhân cả tử và mẫu của mỗi phân số nhân với tích hai mẫu số của hai phân số còn lại.

Ta thực hiện như sau:

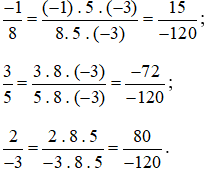
Mẫu số chung của ba phân số trên là −120.

2. Tính chất 2

Tính chất 2: Nếu chia cả tử và mẫu của một phân số cho cùng một ước chung của chúng thì ta được một phân số mới bằng phân số đã cho.

Ví dụ 5. Cho phân số 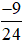. Chia cả tử và mẫu của phân số  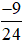cho 3, ta được:

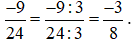
Khi đó, ta có phân số mới là 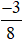 bằng phân số đã cho là .

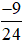Áp dụng tính chất 2, ta có thể rút gọn phân số bằng cách chia cả tử và mẫu cho cùng ước chung khác 1 và −1.

Ví dụ 6. Rút gọn phân số .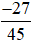

Lời giải: 

Chia cả tử và mẫu của phân số 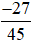 cho 9, ta được:

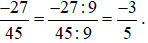
Nhận xét: Sau khi rút gọn ta được phân số mới là 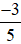 bằng phân số đã cho là .

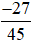Chú ý: Khi rút gọn phân số, có thể được nhiều kết quả, nhưng các phân số ở các kết quả đó đều bằng nhau.

Ví dụ 7. Rút gọn phân số .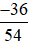

Lời giải: 

Chia cả tử và mẫu của phân số 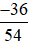 cho 2, ta được:

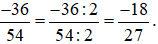
Chia cả tử và mẫu của phân số 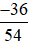 cho 3, ta được:

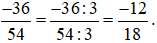
Chia cả tử và mẫu của phân số 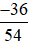 cho 6, ta được:

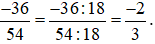
Nhận xét: Khi rút gọn phân số 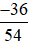, ta thu được nhiều kết quả như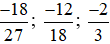  

Các phân số 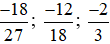 đều bằng nhau.

Tổng quát: .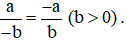

Chú ý: Mỗi phân số đều có nhiều phân số bằng nó.

Ví dụ 8. Viết phân số 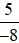 thành phân số có mẫu dương.

Lời giải: 

Phân số 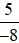 có mẫu là số nguyên âm. 

Do đó để viết phân số 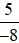 thành phân số có mẫu dương thì ta chia cả tử và mẫu của phân số này cho cùng một số nguyên âm và là ước chung của 5 và (−8) là (−1).

Khi đó ta có:

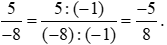
Vậy phân số 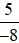 được viết thành phân số có mẫu dương là .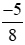