A. \[\frac{2}{{ - 3}} >\,\,\frac{{ - 7}}{8}\]
B. \[\frac{{ - 22}}{{33}} = \frac{{200}}{{ - 300}}\]
C. \[ - \frac{2}{5} < \frac{{196}}{{294}}\]
D. \[\frac{{ - 3}}{5} < \,\frac{{39}}{{ - 65}}\]
Giải bởi Vietjack
Đáp án A: Ta có:
\[\frac{2}{{ - 3}} = \frac{{ - 2}}{3} = \frac{{ - 2.8}}{{3.8}} = \frac{{ - 16}}{{24}};\frac{{ - 7}}{8} = \frac{{ - 7.3}}{{8.3}} = \frac{{ - 21}}{{24}}\]
Vì \[\frac{{ - 16}}{{24}} >\frac{{ - 21}}{{24}}\] nên suy ra \[\frac{2}{{ - 3}} >\,\,\,\frac{{ - 7}}{8}\] nên A đúng.
Đáp án B: Ta có:
\[\frac{{ - 22}}{{33}} = \frac{{ - 22:11}}{{33:11}} = \frac{{ - 2}}{3};\,\,\,\,\,\,\,\,\,\frac{{200}}{{ - 300}} = \frac{{ - 200}}{{300}} = \frac{{ - 200:100}}{{300:100}} = \frac{{ - 2}}{3}\]
Vì \[\frac{{ - 2}}{3} = \frac{{ - 2}}{3}\]nên suy ra \[\frac{{ - 22}}{{33}} = \frac{{200}}{{ - 300}}\] nên B đúng.
Đáp án C: Ta có:
\[ - \frac{2}{5} < 0\,;\frac{{196}}{{294}}\, >0 \Rightarrow \frac{{ - 2}}{5} nên C đúng.
Đáp án D: Ta có:
\[\frac{{39}}{{ - 65}} = \frac{{39:( - 13)}}{{( - 65):( - 13)}} = \frac{{ - 3}}{5}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\]
Vì \[\frac{{ - 3}}{5} = \frac{{ - 3}}{5}\]nên suy ra \[\frac{{ - 3}}{5} = \,\frac{{39}}{{ - 65}}\] nên D sai.
Đáp án cần chọn là: D
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
1. So sánh hai phân số có cùng mẫu
Quy tắc 1. Với hai phân số có cùng một mẫu dương: Phân số nào có tử số nhỏ hơn thì phân số đó nhỏ hơn, phân số nào có tử số lớn hơn thì phân số đó lớn hơn.
Ví dụ 1. So sánh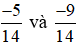 
.
Lời giải:
Ta có −5 > −9 và 14 > 0 nên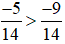 
.
Chú ý: Với hai phân số có cùng một mẫu nguyên âm, ta đưa chúng về hai phân số có cùng mẫu nguyên dương rồi so sánh.
Ví dụ 2. So sánh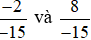 
.
Lời giải:
Đưa hai phân số về cùng mẫu dương, ta được:
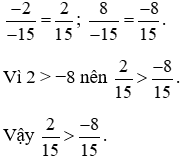
2. So sánh hai phân số khác mẫu
Quy tắc 2. Để so sánh hai phân số có mẫu khác nhau, ta viết hai phân số đó ở dạng hai phân số có cùng một mẫu dương rồi so sánh hai phân số mới nhận được.
Ví dụ 3. So sánh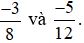 
.
Lời giải:
Mẫu số chung = BCNN (8; 12) = 24.
Ta thực hiện
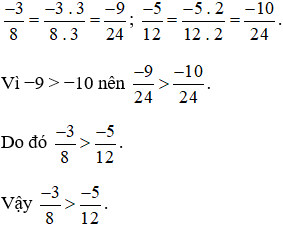
3. Áp dụng quy tắc so sánh phân số
Nhờ viết số nguyên dưới dạng phân số, ta so sánh được số nguyên với phân số.
Ví dụ 4. Viết số nguyên dưới dạng phân số rồi so sánh hai số sau: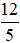 
và 3.
Lời giải:
a) Ta có: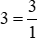 
.
Mẫu số chung là: 5.
Ta thực hiện: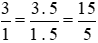 
và giữ nguyên phân số .
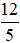Vì 15 > 12 nên
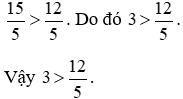
Chú ý: Khi so sánh phân số ta có thể áp dụng tính chất bắc cầu. Nghĩa là:
Nếu có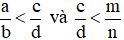 
thì ta có 
.
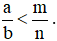Ví dụ 5. So sánh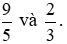 
.
Lời giải:
Phân số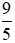 
có tử số là 9 lớn hơn mẫu số là 5 nên 
.
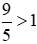Phân số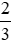 
có tử số là 2 nhỏ hơn mẫu số là 3 nên 
.
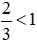Do đó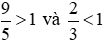 
.
Theo tính chất bắc cầu, ta suy ra:
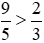
Nhận xét:
- Phân số nhỏ hơn số 0 gọi là phân số âm. Phân số lớn hơn số 0 là phân số dương.
- Theo tính chất bắc cầu, phân số âm nhỏ hơn phân số dương.
Ví dụ 6. So sánh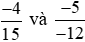 
.
Lời giải:
Ta có: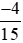 
là phân số âm vì phân số có tử số và mẫu số trái dấu nên 
.
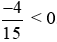Và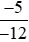 
là phân số dương vì phân số có tử số và mẫu số cùng dấu nên 
.
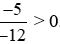Áp dụng tính chất bắc cầu, ta suy ra: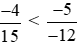 
.
Vậy .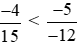
Một hộp có 5 chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số 1, 2, 3, 4, 5; hai thẻ khác nhau thì ghi số khác nhau. Rút ngẫu nhiên một thẻ rồi bỏ lại thẻ vào hộp.
Sau 25 lần rút thẻ liên tiếp, hãy ghi kết quả thống kê theo mẫu sau:
|
Lần 1 |
Số 3 |
Lần 6 |
Số 5 |
Lần 11 |
Số 3 |
Lần 16 |
Số 2 |
Lần 21 |
Số 1 |
|
Lần 2 |
Số 1 |
Lần 7 |
Số 2 |
Lần 12 |
Số 2 |
Lần 17 |
Số 1 |
Lần 22 |
Số 5 |
|
Lần 3 |
Số 2 |
Lần 8 |
Số 3 |
Lần 13 |
Số 2 |
Lần 18 |
Số 2 |
Lần 23 |
Số 3 |
|
Lần 4 |
Số 3 |
Lần 9 |
Số 4 |
Lần 14 |
Số 1 |
Lần 19 |
Số 3 |
Lần 24 |
Số 4 |
|
Lần 5 |
Số 4 |
Lần 10 |
Số 5 |
Lần 15 |
Số 5 |
Lần 20 |
Số 5 |
Lần 25 |
Số 5 |
Tính xác suất thực nghiệm
Xuất hiện số chẵn
Một hộp có 5 chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số 1, 2, 3, 4, 5; hai thẻ khác nhau thì ghi số khác nhau. Rút ngẫu nhiên một thẻ rồi bỏ lại thẻ vào hộp.
Sau 25 lần rút thẻ liên tiếp, hãy ghi kết quả thống kê theo mẫu sau:
|
Lần 1 |
Số 3 |
Lần 6 |
Số 5 |
Lần 11 |
Số 3 |
Lần 16 |
Số 2 |
Lần 21 |
Số 1 |
|
Lần 2 |
Số 1 |
Lần 7 |
Số 2 |
Lần 12 |
Số 2 |
Lần 17 |
Số 1 |
Lần 22 |
Số 5 |
|
Lần 3 |
Số 2 |
Lần 8 |
Số 3 |
Lần 13 |
Số 2 |
Lần 18 |
Số 2 |
Lần 23 |
Số 3 |
|
Lần 4 |
Số 3 |
Lần 9 |
Số 4 |
Lần 14 |
Số 1 |
Lần 19 |
Số 3 |
Lần 24 |
Số 4 |
|
Lần 5 |
Số 4 |
Lần 10 |
Số 5 |
Lần 15 |
Số 5 |
Lần 20 |
Số 5 |
Lần 25 |
Số 5 |
Tính xác suất thực nghiệm
Xuất hiện số 2
Một hộp có 5 chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số 1, 2, 3, 4, 5; hai thẻ khác nhau thì ghi số khác nhau. Rút ngẫu nhiên một thẻ rồi bỏ lại thẻ vào hộp.
Sau 25 lần rút thẻ liên tiếp, hãy ghi kết quả thống kê theo mẫu sau:
|
Lần 1 |
Số 3 |
Lần 6 |
Số 5 |
Lần 11 |
Số 3 |
Lần 16 |
Số 2 |
Lần 21 |
Số 1 |
|
Lần 2 |
Số 1 |
Lần 7 |
Số 2 |
Lần 12 |
Số 2 |
Lần 17 |
Số 1 |
Lần 22 |
Số 5 |
|
Lần 3 |
Số 2 |
Lần 8 |
Số 3 |
Lần 13 |
Số 2 |
Lần 18 |
Số 2 |
Lần 23 |
Số 3 |
|
Lần 4 |
Số 3 |
Lần 9 |
Số 4 |
Lần 14 |
Số 1 |
Lần 19 |
Số 3 |
Lần 24 |
Số 4 |
|
Lần 5 |
Số 4 |
Lần 10 |
Số 5 |
Lần 15 |
Số 5 |
Lần 20 |
Số 5 |
Lần 25 |
Số 5 |
Tính xác suất thực nghiệm
Xuất hiện số 1
