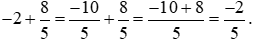A. \[x = \frac{{21}}{{20}}\]
B. \[x = \frac{{29}}{{20}}\]
C. \[x = \frac{{ - 3}}{{10}}\]
D. \[x = \frac{{ - 9}}{{10}}\]
Giải bởi Vietjack
\[x - \frac{1}{5} = 2 + \frac{{ - 3}}{4}\]
\[x - \frac{1}{5} = \frac{5}{4}\]
\[x = \frac{5}{4} + \frac{1}{5}\]
\[x = \frac{{29}}{{20}}\]
Đáp án cần chọn là: B
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
1. Phép cộng hai phân số
Quy tắc cộng hai hai phân số cùng mẫu: Muốn cộng hai phân số có cùng mẫu số, ta cộng tử số với nhau và giữ nguyên mẫu số.
Ví dụ 1. Tính: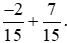 
.
Lời giải:
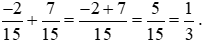
Quy tắc cộng hai phân số khác mẫu: Muốn cộng hai phân số khác mẫu, ta quy đồng mẫu số của chúng
Ví dụ 2. Tính: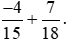 
.
Lời giải:
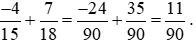
2. Một số tính chất của phép cộng phân số
Phép cộng phân số có các tính chất giao hoán và kết hợp, cộng một phân số với 0 ta được chính nó.
Ví dụ 3. Tính biểu thức sau theo cách hợp lí: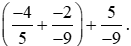 
.
Lời giải:
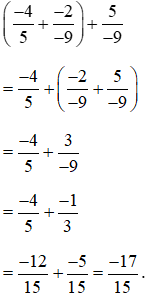
3. Số đối
Hai phân số là đối nhau nếu tổng của chúng bằng 0.
Kí hiệu số đối của phân số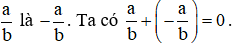 
.
Mà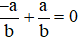 
nên ta có: 
.
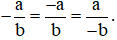Ví dụ 4. Tìm số đối của mỗi phân số sau (có dùng kí hiệu số đối của phân số).
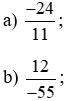
Lời giải:
a) Số đối của phân số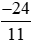 
là phân số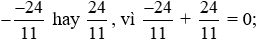 
b) Số đối của phân số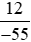 
là phân số 
.
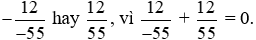4. Phép trừ hai phân số
Muốn trừ một phân số cho một phân số, ta lấy phân số thứ nhất cộng với số đối của phân số thứ hai.
Ví dụ 5. Thực hiện phép tính: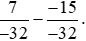 
.
Lời giải:
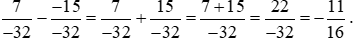
Quy tắc dấu ngoặc:
- Khi bỏ ngoặc có dấu cộng (+) đằng trước, ta giữ nguyên dấu các số hạng trong ngoặc.
- Khi bỏ ngoặc có dấu trừ (−) đằng trước, ta phải đổi dấu tất cả các số hạng trong ngoặc.
Ví dụ 6.
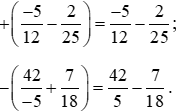
Chú ý: Ta thực hiện được phép cộng và phép trừ phân số với số nguyên bằng cách viết số nguyên ở dạng phân số.
Ví dụ 7. Tính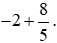 
.
Lời giải:
Một hộp có 5 chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số 1, 2, 3, 4, 5; hai thẻ khác nhau thì ghi số khác nhau. Rút ngẫu nhiên một thẻ rồi bỏ lại thẻ vào hộp.
Sau 25 lần rút thẻ liên tiếp, hãy ghi kết quả thống kê theo mẫu sau:
|
Lần 1 |
Số 3 |
Lần 6 |
Số 5 |
Lần 11 |
Số 3 |
Lần 16 |
Số 2 |
Lần 21 |
Số 1 |
|
Lần 2 |
Số 1 |
Lần 7 |
Số 2 |
Lần 12 |
Số 2 |
Lần 17 |
Số 1 |
Lần 22 |
Số 5 |
|
Lần 3 |
Số 2 |
Lần 8 |
Số 3 |
Lần 13 |
Số 2 |
Lần 18 |
Số 2 |
Lần 23 |
Số 3 |
|
Lần 4 |
Số 3 |
Lần 9 |
Số 4 |
Lần 14 |
Số 1 |
Lần 19 |
Số 3 |
Lần 24 |
Số 4 |
|
Lần 5 |
Số 4 |
Lần 10 |
Số 5 |
Lần 15 |
Số 5 |
Lần 20 |
Số 5 |
Lần 25 |
Số 5 |
Tính xác suất thực nghiệm
Xuất hiện số chẵn
Một hộp có 5 chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số 1, 2, 3, 4, 5; hai thẻ khác nhau thì ghi số khác nhau. Rút ngẫu nhiên một thẻ rồi bỏ lại thẻ vào hộp.
Sau 25 lần rút thẻ liên tiếp, hãy ghi kết quả thống kê theo mẫu sau:
|
Lần 1 |
Số 3 |
Lần 6 |
Số 5 |
Lần 11 |
Số 3 |
Lần 16 |
Số 2 |
Lần 21 |
Số 1 |
|
Lần 2 |
Số 1 |
Lần 7 |
Số 2 |
Lần 12 |
Số 2 |
Lần 17 |
Số 1 |
Lần 22 |
Số 5 |
|
Lần 3 |
Số 2 |
Lần 8 |
Số 3 |
Lần 13 |
Số 2 |
Lần 18 |
Số 2 |
Lần 23 |
Số 3 |
|
Lần 4 |
Số 3 |
Lần 9 |
Số 4 |
Lần 14 |
Số 1 |
Lần 19 |
Số 3 |
Lần 24 |
Số 4 |
|
Lần 5 |
Số 4 |
Lần 10 |
Số 5 |
Lần 15 |
Số 5 |
Lần 20 |
Số 5 |
Lần 25 |
Số 5 |
Tính xác suất thực nghiệm
Xuất hiện số 2
Một hộp có 5 chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số 1, 2, 3, 4, 5; hai thẻ khác nhau thì ghi số khác nhau. Rút ngẫu nhiên một thẻ rồi bỏ lại thẻ vào hộp.
Sau 25 lần rút thẻ liên tiếp, hãy ghi kết quả thống kê theo mẫu sau:
|
Lần 1 |
Số 3 |
Lần 6 |
Số 5 |
Lần 11 |
Số 3 |
Lần 16 |
Số 2 |
Lần 21 |
Số 1 |
|
Lần 2 |
Số 1 |
Lần 7 |
Số 2 |
Lần 12 |
Số 2 |
Lần 17 |
Số 1 |
Lần 22 |
Số 5 |
|
Lần 3 |
Số 2 |
Lần 8 |
Số 3 |
Lần 13 |
Số 2 |
Lần 18 |
Số 2 |
Lần 23 |
Số 3 |
|
Lần 4 |
Số 3 |
Lần 9 |
Số 4 |
Lần 14 |
Số 1 |
Lần 19 |
Số 3 |
Lần 24 |
Số 4 |
|
Lần 5 |
Số 4 |
Lần 10 |
Số 5 |
Lần 15 |
Số 5 |
Lần 20 |
Số 5 |
Lần 25 |
Số 5 |
Tính xác suất thực nghiệm
Xuất hiện số 1
