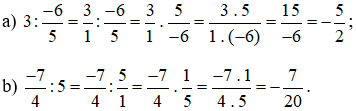A. \[\frac{7}{{18}}\]
B. \[\frac{9}{{14}}\]
C. \[\frac{{36}}{7}\]
D. \[\frac{{18}}{7}\]
 Giải bởi Vietjack
Giải bởi Vietjack
\[\frac{2}{3}:\frac{7}{{12}}:\frac{4}{{18}}\]
\[ = \left( {\frac{2}{3}:\frac{7}{{12}}} \right):\frac{4}{{18}}\]
\[ = \left( {\frac{2}{3}.\frac{{12}}{7}} \right):\frac{4}{{18}}\]
\[ = \frac{8}{7}:\frac{4}{{18}}\]
\[ = \frac{8}{7}.\frac{{18}}{4}\]
\[ = \frac{{36}}{7}\]
Đáp án cần chọn là: C
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết

Điền số thích hợp vào ô trống
Độ cao của đáy vịnh Cam Ranh là -32 m. Độ cao của đáy sông Sài Gòn bằng \(\frac{5}{8}\) ở độ cao của đáy vịnh Cam Ranh. Vậy độ cao của đáy sông Sài Gòn là  mét
mét

Điền số thích hợp vào ô trống
Bạn Hoà đã đọc hết một cuốn truyện dày 80 trang trong ba ngày. Biết ngày thứ nhất bạn Hoà đọc được \(\frac{3}{8}\) số trang cuốn truyện, ngày thứ hai đọc được \(\frac{2}{5}\) số trang cuốn truyện. Số trang bạn Hoà đã đọc được trong ngày thứ ba là  trang
trang
\[\left( {\frac{{20}}{7}.\frac{{ - 4}}{{ - 5}}} \right) + \left( {\frac{{20}}{7}.\frac{3}{{ - 5}}} \right)\]
1. Nhân hai phân số
Quy tắc: Muốn nhân hai phân số, ta nhân tử số với nhau và nhân hai mẫu số với nhau.
Ví dụ 1. Tính 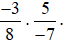 .
.
Lời giải:
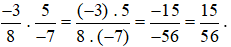
2. Một số tính chất của phép nhân phân số
Phép nhân phân số có các tính chất: giao hoán, kết hợp, phân phối của phép nhân đối với phép cộng.
Chú ý: Khi nhân một phân số với 1 ta được chính nó.
Ví dụ 2. Tính giá trị biểu thức 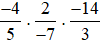 theo cách hợp lí.
theo cách hợp lí.
Lời giải:
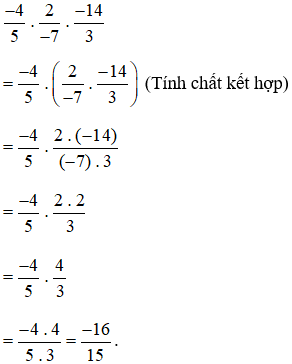
3. Chia phân số
Quy tắc chia phân số: Muốn chia một phân số cho một phân số khác 0 ta nhân phân số thứ nhất với phân số có tử số là mẫu số của phân số thứ hai và mẫu số là tử số của phân số thứ nhất.
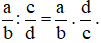
Ví dụ 3. Tính 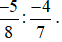 .
.
Lời giải:
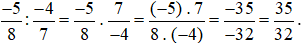
Chú ý: Ta thực hiện được phép nhân và phép chia phân số với số nguyên bằng cách viết số nguyên dưới dạng phân số.
Ví dụ 4. Tính:
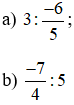
Lời giải: