A.90m
B.224m
C.84m
D.112 m
Giải bởi Vietjack
Phân số chỉ số vải còn lại của tấm thứ 1 là: \[1 - \frac{3}{7} = \frac{4}{7}\] (tấm thứ nhất)
Phân số chỉ số vải còn lại của tấm thứ 2 là: \[1 - \frac{1}{5} = \frac{4}{5}\] (tấm thứ hai)
Phân số chỉ số vải còn lại của tấm thứ 3 là: \[1 - \frac{2}{5} = \frac{3}{5}\] (tấm thứ ba)
Tỉ số giữa số mét vải tấm thứ hai và thứ nhất là: \[\frac{4}{7}:\frac{4}{5} = \frac{5}{7}\]
Tỉ số giữa số mét vải tấm thứ ba và thứ nhất là: \[\frac{4}{7}:\frac{3}{5} = \frac{{20}}{{21}}\] 224m vải ứng với số phần tấm thứ nhất là: \[1 + \frac{5}{7} + \frac{{20}}{{21}} = \frac{8}{3}\]
Tấm thứ nhất dài là: \[224:\frac{8}{3} = 84\left( m \right)\] Vậy tấm thứ nhất dài 84m.
Đáp án cần chọn là: C
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Bác đem \(\frac{4}{5}\) ở số cà chua đó đi bán, giá mỗi ki-lô-gam cà chua là 12 500 đồng. Hỏi bác nông dân nhận được bao nhiêu tiền?
Một bể nuôi cá cảnh dạng khối hộp chữ nhật, có kích thước 30 cm x 40 cm và chiều cao 20cm. Lượng nước trong bể cao bằng \(\frac{3}{4}\) chiều cao của bể. Tính số lít nước ở bể đó.
Điền số thích hợp vào ô trống
Gấu túi là một loài thú có túi, ăn thực vật, sống ở một số bang của Ô-xtrây-li-a. Nó có chiều dài cơ thể từ 60 cm đến 85 cm và khối lượng từ 4 kg đến 15 kg. Màu lông từ xám bạc đến nâu sô-cô-la. Gấu túi hoạt động vào ban đêm, thức ăn chủ yếu là một vài loại lá cây bạch đàn, khuynh diệp.
Gấu túi dành \(\frac{3}{4}\) thời gian trong ngày để ngủ. Con người dùng \(\frac{1}{3}\) thời gian trong ngày để ngủ. Trong một ngày gấu túi ngủ nhiều hơn con người 
giờ
1. Tính giá trị phân số của một số
Quy tắc 1: Muốn tính giá trị phân số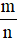 
của số a, ta tính 
.
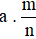Ví dụ 1. Tính giá trị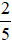 
của 120.
Lời giải:
Giá trị 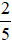của 120 là:
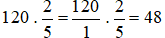
Vậy số cần tìm là 48.
2. Tìm một số khi biết giá trị phân số của số đó
Quy tắc 2: Muốn tìm một số khi biết giá trị phân số 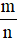của nó là b, ta tính 
.
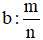Ví dụ 2. Tìm một số, biết 
của số đó là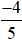 
.
Lời giải:
Giá trị phân số của số đó là thì số đó là: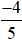
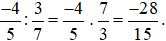
Vậy số cần tìm là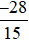 
.
Một hộp có 5 chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số 1, 2, 3, 4, 5; hai thẻ khác nhau thì ghi số khác nhau. Rút ngẫu nhiên một thẻ rồi bỏ lại thẻ vào hộp.
Sau 25 lần rút thẻ liên tiếp, hãy ghi kết quả thống kê theo mẫu sau:
|
Lần 1 |
Số 3 |
Lần 6 |
Số 5 |
Lần 11 |
Số 3 |
Lần 16 |
Số 2 |
Lần 21 |
Số 1 |
|
Lần 2 |
Số 1 |
Lần 7 |
Số 2 |
Lần 12 |
Số 2 |
Lần 17 |
Số 1 |
Lần 22 |
Số 5 |
|
Lần 3 |
Số 2 |
Lần 8 |
Số 3 |
Lần 13 |
Số 2 |
Lần 18 |
Số 2 |
Lần 23 |
Số 3 |
|
Lần 4 |
Số 3 |
Lần 9 |
Số 4 |
Lần 14 |
Số 1 |
Lần 19 |
Số 3 |
Lần 24 |
Số 4 |
|
Lần 5 |
Số 4 |
Lần 10 |
Số 5 |
Lần 15 |
Số 5 |
Lần 20 |
Số 5 |
Lần 25 |
Số 5 |
Tính xác suất thực nghiệm
Xuất hiện số chẵn
Một hộp có 5 chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số 1, 2, 3, 4, 5; hai thẻ khác nhau thì ghi số khác nhau. Rút ngẫu nhiên một thẻ rồi bỏ lại thẻ vào hộp.
Sau 25 lần rút thẻ liên tiếp, hãy ghi kết quả thống kê theo mẫu sau:
|
Lần 1 |
Số 3 |
Lần 6 |
Số 5 |
Lần 11 |
Số 3 |
Lần 16 |
Số 2 |
Lần 21 |
Số 1 |
|
Lần 2 |
Số 1 |
Lần 7 |
Số 2 |
Lần 12 |
Số 2 |
Lần 17 |
Số 1 |
Lần 22 |
Số 5 |
|
Lần 3 |
Số 2 |
Lần 8 |
Số 3 |
Lần 13 |
Số 2 |
Lần 18 |
Số 2 |
Lần 23 |
Số 3 |
|
Lần 4 |
Số 3 |
Lần 9 |
Số 4 |
Lần 14 |
Số 1 |
Lần 19 |
Số 3 |
Lần 24 |
Số 4 |
|
Lần 5 |
Số 4 |
Lần 10 |
Số 5 |
Lần 15 |
Số 5 |
Lần 20 |
Số 5 |
Lần 25 |
Số 5 |
Tính xác suất thực nghiệm
Xuất hiện số 2
Một hộp có 5 chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số 1, 2, 3, 4, 5; hai thẻ khác nhau thì ghi số khác nhau. Rút ngẫu nhiên một thẻ rồi bỏ lại thẻ vào hộp.
Sau 25 lần rút thẻ liên tiếp, hãy ghi kết quả thống kê theo mẫu sau:
|
Lần 1 |
Số 3 |
Lần 6 |
Số 5 |
Lần 11 |
Số 3 |
Lần 16 |
Số 2 |
Lần 21 |
Số 1 |
|
Lần 2 |
Số 1 |
Lần 7 |
Số 2 |
Lần 12 |
Số 2 |
Lần 17 |
Số 1 |
Lần 22 |
Số 5 |
|
Lần 3 |
Số 2 |
Lần 8 |
Số 3 |
Lần 13 |
Số 2 |
Lần 18 |
Số 2 |
Lần 23 |
Số 3 |
|
Lần 4 |
Số 3 |
Lần 9 |
Số 4 |
Lần 14 |
Số 1 |
Lần 19 |
Số 3 |
Lần 24 |
Số 4 |
|
Lần 5 |
Số 4 |
Lần 10 |
Số 5 |
Lần 15 |
Số 5 |
Lần 20 |
Số 5 |
Lần 25 |
Số 5 |
Tính xác suất thực nghiệm
Xuất hiện số 1
