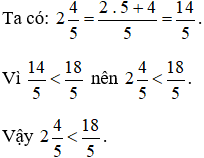Người ta mở vòi cho nước chảy vào đầy bể cần 3 giờ. Hỏi nếu mở vòi nước đó trong 45 phút thì được bao nhiêu phần của bể?
A. \[\frac{1}{3}\]
B. \[\frac{1}{4}\]
C. \[\frac{2}{3}\]
D. \[\frac{1}{2}\]
Giải bởi Vietjack
Đổi: 45phút =\[\frac{3}{4}\] giờ
Mỗi giờ vòi nước chảy được số phần bể là: \[1:3 = \frac{1}{3}\] (bể)
Nếu mở vòi trong 45 phút thì được số phần bể là: \[\frac{3}{4}.\frac{1}{3} = \frac{1}{4}\] (bể)
Đáp án cần chọn là: B
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Lúc 7 giờ 5 phút, một người đi xe máy đi từ A và đến B lúc 8 giờ 45 phút. Biết quãng đường AB dài 65km. Tính vận tốc của người đi xe máy đó?
Sắp xếp các phân số sau: \[\frac{1}{3};\frac{1}{2};\frac{3}{8};\frac{6}{7}\] theo thứ tự từ lớn đến bé.
Rút gọn phân số \[\;\frac{{1978.1979 + 1980.21 + 1958}}{{1980.1979 - 1978.1979}}\] ta được kết quả là:
Cho hai biểu thức \[B = \,\,\left( {\frac{2}{3} - 1\frac{1}{2}} \right):\frac{4}{3} + \frac{1}{2}\] và \[C = \,\frac{9}{{23}}.\frac{5}{8} + \frac{9}{{23}}.\frac{3}{8} - \frac{9}{{23}}\] . Chọn câu đúng
Không qui đồng, hãy so sánh hai phân số sau: \[\frac{{37}}{{67}}\] và \[\frac{{377}}{{677}}\] .
Tính nhanh \[A = \frac{5}{{1.3}} + \frac{5}{{3.5}} + \frac{5}{{5.7}} + ... + \frac{5}{{99.101}}\]
Cho \[A = \frac{{\left( {3\frac{2}{{15}} + \frac{1}{5}} \right):2\frac{1}{2}}}{{\left( {5\frac{3}{7} - 2\frac{1}{4}} \right):4\frac{{43}}{{56}}}}\] và \[B = \frac{{1,2:\left( {1\frac{1}{5}.1\frac{1}{4}} \right)}}{{0,32 + \frac{2}{{25}}}}\] . Chọn đáp án đúng.
Cho phân số \[A = \frac{{n - 5}}{{n + 1}}\,\,\left( {n \in Z;n \ne - 1} \right)\] dụng
Tìm điều kiện của n để A là phân số tối giản.
Tìm một phân số ở giữa hai phân số \(\frac{1}{{10}}\) và \(\frac{2}{{10}}\) .
Cho a và b là hai số nguyên dương, a > b, a không chia hết cho b. Nếu a chia cho b được thương là q và số dư là r, thì ta viết 
và gọi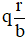 
là hỗn số.
Ví dụ 1. Cho hai số nguyên dương là 25 và 3; 25 > 3 và 25 không chia hết cho 3.
Thực hiện phép chia 25 cho 3 được thương là 8 và số dư là 1.
Khi đó,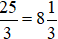 
. Đọc là “tám, một phần ba”.
Chú ý: Với hỗn số 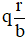người ta gọi q là phần số nguyên và 
là phần phân số của hỗn số.
Ví dụ 2. Viết phân số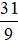 
dưới dạng hỗn số và cho biết phần số nguyên, phần phân số.
Lời giải:
Thực hiện phép chia 31 cho 9 được thương là 3 và số dư là 4.
Khi đó,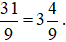 
.
Trong đó, phần số nguyên là 3 và phần phân số là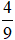 
.
Vậy phân số 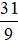dưới dạng hỗn số là 
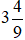và phần số nguyên là 3, phần phân số là .
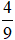2. Đổi hỗn số ra phân số
Ta biết viết phân số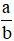 
với a > b > 0 thành hỗn số .
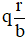Ngược lại, ta đổi được hỗn số 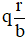thành phân số, theo quy tắc sau:
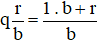
Ví dụ 3. So sánh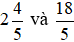 
.
Lời giải:
Một hộp có 5 chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số 1, 2, 3, 4, 5; hai thẻ khác nhau thì ghi số khác nhau. Rút ngẫu nhiên một thẻ rồi bỏ lại thẻ vào hộp.
Sau 25 lần rút thẻ liên tiếp, hãy ghi kết quả thống kê theo mẫu sau:
|
Lần 1 |
Số 3 |
Lần 6 |
Số 5 |
Lần 11 |
Số 3 |
Lần 16 |
Số 2 |
Lần 21 |
Số 1 |
|
Lần 2 |
Số 1 |
Lần 7 |
Số 2 |
Lần 12 |
Số 2 |
Lần 17 |
Số 1 |
Lần 22 |
Số 5 |
|
Lần 3 |
Số 2 |
Lần 8 |
Số 3 |
Lần 13 |
Số 2 |
Lần 18 |
Số 2 |
Lần 23 |
Số 3 |
|
Lần 4 |
Số 3 |
Lần 9 |
Số 4 |
Lần 14 |
Số 1 |
Lần 19 |
Số 3 |
Lần 24 |
Số 4 |
|
Lần 5 |
Số 4 |
Lần 10 |
Số 5 |
Lần 15 |
Số 5 |
Lần 20 |
Số 5 |
Lần 25 |
Số 5 |
Tính xác suất thực nghiệm
Xuất hiện số chẵn
Một hộp có 5 chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số 1, 2, 3, 4, 5; hai thẻ khác nhau thì ghi số khác nhau. Rút ngẫu nhiên một thẻ rồi bỏ lại thẻ vào hộp.
Sau 25 lần rút thẻ liên tiếp, hãy ghi kết quả thống kê theo mẫu sau:
|
Lần 1 |
Số 3 |
Lần 6 |
Số 5 |
Lần 11 |
Số 3 |
Lần 16 |
Số 2 |
Lần 21 |
Số 1 |
|
Lần 2 |
Số 1 |
Lần 7 |
Số 2 |
Lần 12 |
Số 2 |
Lần 17 |
Số 1 |
Lần 22 |
Số 5 |
|
Lần 3 |
Số 2 |
Lần 8 |
Số 3 |
Lần 13 |
Số 2 |
Lần 18 |
Số 2 |
Lần 23 |
Số 3 |
|
Lần 4 |
Số 3 |
Lần 9 |
Số 4 |
Lần 14 |
Số 1 |
Lần 19 |
Số 3 |
Lần 24 |
Số 4 |
|
Lần 5 |
Số 4 |
Lần 10 |
Số 5 |
Lần 15 |
Số 5 |
Lần 20 |
Số 5 |
Lần 25 |
Số 5 |
Tính xác suất thực nghiệm
Xuất hiện số 2
Một hộp có 5 chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số 1, 2, 3, 4, 5; hai thẻ khác nhau thì ghi số khác nhau. Rút ngẫu nhiên một thẻ rồi bỏ lại thẻ vào hộp.
Sau 25 lần rút thẻ liên tiếp, hãy ghi kết quả thống kê theo mẫu sau:
|
Lần 1 |
Số 3 |
Lần 6 |
Số 5 |
Lần 11 |
Số 3 |
Lần 16 |
Số 2 |
Lần 21 |
Số 1 |
|
Lần 2 |
Số 1 |
Lần 7 |
Số 2 |
Lần 12 |
Số 2 |
Lần 17 |
Số 1 |
Lần 22 |
Số 5 |
|
Lần 3 |
Số 2 |
Lần 8 |
Số 3 |
Lần 13 |
Số 2 |
Lần 18 |
Số 2 |
Lần 23 |
Số 3 |
|
Lần 4 |
Số 3 |
Lần 9 |
Số 4 |
Lần 14 |
Số 1 |
Lần 19 |
Số 3 |
Lần 24 |
Số 4 |
|
Lần 5 |
Số 4 |
Lần 10 |
Số 5 |
Lần 15 |
Số 5 |
Lần 20 |
Số 5 |
Lần 25 |
Số 5 |
Tính xác suất thực nghiệm
Xuất hiện số 1
