A. \[ - \frac{{21}}{4}\]
B. \[ - \frac{{11}}{4}\]
C. \[ - \frac{{10}}{4}\]
D. \[ - \frac{5}{4}\]
 Giải bởi Vietjack
Giải bởi Vietjack
\[ - 2\frac{3}{4} = - \frac{{2.4 + 3}}{4} = - \frac{{11}}{4}\]
Đáp án cần chọn là: B
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
−120,341; 36,095; 36,1; −120,34.
−0,125 =…; −0,012 =...; −4,005 =...

Trong một cuộc thi chạy 200 m, có ba vận động viên đạt thành tích cao nhất là:
Mai Anh: 31,42 giây; Ngọc Mai: 31,48 giây; Phương Hà: 31,09 giây.
Các vận động viên đã về Nhất, về Nhì, về Ba lần lượt là:
\[\frac{{ - 9}}{{1000}} = ...;\frac{{ - 5}}{8} = ...;3\frac{2}{{25}} = ...\]
1. Số thập phân âm
- Phân số thập phân là phân số có mẫu số là lũy thừa của 10.
Ví dụ 1. Các phân số 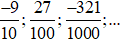 là các phân số thập phân.
là các phân số thập phân.
- Các phân số thập phân dương được viết dưới dạng số thập phân dương.
- Các phân số thập phân âm được viết dưới dạng số thập phân âm.
Ví dụ 2.
0,332; 12,412 là các số thập phân dương.
−3,712; −4,15 là các số thập phân âm.
Số thập phân gồm hai phần:
- Phần số nguyên viết bên trái dấu phẩy;
- Phần thập phân viết bên phải dấu phẩy.
Ví dụ 3.
- Số 42,25 là số thập phân dương có phần số nguyên là 42 và phần thập phân là 25.
- Số −12,316 là số thập phân âm có phần số nguyên là −12 và phần thập phân là 316.
2. Số đối của một số thập phân
Hai số thập phân gọi là đối nhau khi chúng biểu diễn hai phân số thập phân đối nhau.
Ví dụ 4.
- Số đối của 3,45 là −3,45;
- Số đối của −2,36 là 2,36.
3. So sánh hai số thập phân
- Nếu hai số thập phân trái dấu, số thập phân dương lớn hơn số thập phân âm.
- Trong hai số thập phân âm, số nào có số đối lớn hơn thì số đó nhỏ hơn.
Ví dụ 5. Sắp xếp các số thập phân theo thứ tự tăng dần:
−16,25; 8,36; −21,4; 7,24.
Lời giải:
Để sắp xếp các số thập phân sau theo thứ tự tăng dần, ta thực hiện:
Bước 1: Chia thành 2 nhóm số thập dương và số thập phân âm, vì số thập phân âm luôn nhỏ hơn số thập phân dương.
Bước 2: Ta so sánh các số thập phân theo nhóm với nhau:
- Nhóm các số thập phân dương: ta so sánh phần nguyên với nhau, số nào có phần nguyên lớn hơn thì lớn hơn. Nếu phần nguyên bằng nhau thì ta lần lượt so sánh các hàng ở phần thập phân.
- Nhóm các số thập phân âm: ta so sánh số đối của chúng, số nào có số đối lớn hơn thì nhỏ hơn.
Sắp xếp các số thập phân sau theo thứ tự tăng dần:
* Phân loại:
- Nhóm các số thập phân dương: 8,36; 7,24.
- Nhóm các số thập phân âm: −16,25; −21,4.
* So sánh các số thập phân trong theo nhóm:
- Nhóm các số thập phân dương: ta so sánh phần nguyên của các số trên, vì 8 > 7 nên 8,36 > 7,24.
- Nhóm các số thập phân âm: Số đối của các số −16,25; −21,4 lần lượt là 16,25; 21,4.
Ta so sánh phần nguyên của hai số 16,25 và 21,4, vì 16 < 21 nên 16,25 < 21,4.
Hay −16,25 > −21,4.
Do đó −21,4 < −16,25 < 7,24 < 8,36.
Vậy các số được sắp xếp thứ tự tăng dần là: −21,4; −16,25; 7,24; 8,36.