A.\[\frac{{2\frac{{11}}{{12}}}}{{6\frac{1}{8}}} = \frac{{10}}{{21}}\]
B. \[66\frac{2}{3}{\rm{\% }} = \frac{{11}}{{25}}\]
C. \[0,72:2,7 = \frac{4}{{15}}\]
D. \[0,075:5{\rm{\% }} = \frac{3}{2}\]
Giải bởi Vietjack
Đáp án A: \[\frac{{2\frac{{11}}{{12}}}}{{6\frac{1}{8}}} = 2\frac{{11}}{{12}}:6\frac{1}{8} = \frac{{35}}{{12}}:\frac{{49}}{8} = \frac{{35}}{{12}}.\frac{8}{{49}} = \frac{{10}}{{21}}\] nên A đúng.
Đáp án B: \[66\frac{2}{3}{\rm{\% }} = \frac{{200}}{3}:100 = \frac{{200}}{3}.\frac{1}{{100}} = \frac{2}{3}\] nên B sai.
Đáp án C:\[0,72:2,7 = \frac{{72}}{{100}}:\frac{{27}}{{10}} = \frac{{18}}{{25}}.\frac{{10}}{{27}} = \frac{4}{{15}}\] nên C đúng.
Đáp án D: \[0,075:5{\rm{\% }} = \frac{{75}}{{1000}}:\frac{5}{{100}} = \frac{{75}}{{1000}}.\frac{{100}}{5} = \frac{3}{2}\] nên D đúng.
Đáp án cần chọn là: B
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Điền số thích hợp vào ô trống:
Một hình chữ nhật có chu vi là 72cm. Chiều rộng kém chiều dài là 14cm. Vậy tỉ số của chiều rộng và chiều dài là \(\frac{a}{b}\) .
Vậy a = 
; b =
Điền số thích hợp vào ô trống:
Số thứ nhất là số lớn nhất có hai chữ số khác nhau. Số thứ hai là số lẻ nhỏ nhất có ba chữ số khác nhau. Vậy tỉ số của số thứ nhất và số thứ hai là \(\frac{a}{b}\) .
Vậy a = ; b =
Lớp 4A có 15 học sinh nam và 18 học sinh nữ. Viết tỉ số của số học sinh nam và số học sinh cả lớp.
Viết tỉ số phần trăm thành phân số tối giản:
\(72\% = \frac{{......}}{{......}}\)
Điền số thích hợp vào ô trống:
Biết a = 11; b = 15 thì tỉ số của b và a là 
Một hộp đựng 7 quả bóng xanh và 9 quả bóng đỏ. Tỉ số của số quả bóng đỏ và số quả bóng xanh là:
1. Tỉ số của hai đại lượng
Ta gọi thương trong phép chia số a cho số b (b ≠0) là tỉ số của a và b.
Tỉ số của a và b kí hiệu là a : b (cũng kí hiệu là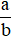 
).
Ví dụ 1.
- Tỉ số của hai số 16 và 37 được kí hiệu là 16 : 37 hay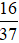 
.
- Tỉ số của hai số 3,6 và 8,25 được kí hiệu là 3,6 : 8,25 hay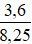 
.
Chú ý:
- Phân số 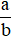thì cả a và b phải là các số nguyên.
- Tỉ số 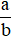thì a và b có thể là các số nguyên, phân số, hỗn số, số thập phân,…
- Ta thường dùng khái niệm tỉ số nói về thương của hai đại lượng cùng loại và cùng đơn vị đo.
Ví dụ 2. Tính tỉ số của hai đại lượng được cho trong các trường hợp sau:
a) 0,6 kg và 260 g;
b) 15 phút và 
giờ.
Lời giải:
a) Đổi 0,6 kg = 600 g
Tỉ số của hai đại lượng 0,4 kg và 340 g hay tỉ số của 400 g và 340 g là:
.
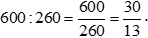Vậy tỉ số của hai đại lượng 0,6 kg và 260 g là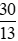 
.
b)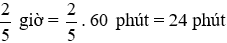 
Tỉ số của hai đại lượng 15 phút và giờ hay tỉ số của 15 phút và 24 phút là:
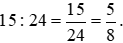
Vậy tỉ số của hai đại lượng 15 phút và giờ là 
.
2. Tỉ số phần trăm của hai đại lượng
Trong thực hành, ta thường dùng tỉ số dưới dạng tỉ số phần trăm với kí hiệu % thay cho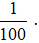 
.
Để tính tỉ số phần trăm của hai số a và b, ta nhân a với 100 rồi chia cho b và viết kí hiệu % vào bên phải kết quả tìm được.
Ví dụ 3. Tính tỉ số phần trăm của hai số cho trong mỗi trường hợp sau:
a) 2 và 8;
b) và 3,125.
Lời giải:
a) Tỉ số phần trăm của hai số 2 và 8 là:
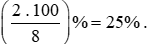
Vậy tỉ số phần trăm của hai số 2 và 8 là 25%.
b) Tỉ số phần trăm của hai số và 3,125 là:
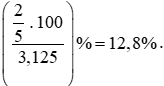
Vậy tỉ số phần trăm của hai số và 3,125 là 12,8%.
Một hộp có 5 chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số 1, 2, 3, 4, 5; hai thẻ khác nhau thì ghi số khác nhau. Rút ngẫu nhiên một thẻ rồi bỏ lại thẻ vào hộp.
Sau 25 lần rút thẻ liên tiếp, hãy ghi kết quả thống kê theo mẫu sau:
|
Lần 1 |
Số 3 |
Lần 6 |
Số 5 |
Lần 11 |
Số 3 |
Lần 16 |
Số 2 |
Lần 21 |
Số 1 |
|
Lần 2 |
Số 1 |
Lần 7 |
Số 2 |
Lần 12 |
Số 2 |
Lần 17 |
Số 1 |
Lần 22 |
Số 5 |
|
Lần 3 |
Số 2 |
Lần 8 |
Số 3 |
Lần 13 |
Số 2 |
Lần 18 |
Số 2 |
Lần 23 |
Số 3 |
|
Lần 4 |
Số 3 |
Lần 9 |
Số 4 |
Lần 14 |
Số 1 |
Lần 19 |
Số 3 |
Lần 24 |
Số 4 |
|
Lần 5 |
Số 4 |
Lần 10 |
Số 5 |
Lần 15 |
Số 5 |
Lần 20 |
Số 5 |
Lần 25 |
Số 5 |
Tính xác suất thực nghiệm
Xuất hiện số chẵn
Một hộp có 5 chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số 1, 2, 3, 4, 5; hai thẻ khác nhau thì ghi số khác nhau. Rút ngẫu nhiên một thẻ rồi bỏ lại thẻ vào hộp.
Sau 25 lần rút thẻ liên tiếp, hãy ghi kết quả thống kê theo mẫu sau:
|
Lần 1 |
Số 3 |
Lần 6 |
Số 5 |
Lần 11 |
Số 3 |
Lần 16 |
Số 2 |
Lần 21 |
Số 1 |
|
Lần 2 |
Số 1 |
Lần 7 |
Số 2 |
Lần 12 |
Số 2 |
Lần 17 |
Số 1 |
Lần 22 |
Số 5 |
|
Lần 3 |
Số 2 |
Lần 8 |
Số 3 |
Lần 13 |
Số 2 |
Lần 18 |
Số 2 |
Lần 23 |
Số 3 |
|
Lần 4 |
Số 3 |
Lần 9 |
Số 4 |
Lần 14 |
Số 1 |
Lần 19 |
Số 3 |
Lần 24 |
Số 4 |
|
Lần 5 |
Số 4 |
Lần 10 |
Số 5 |
Lần 15 |
Số 5 |
Lần 20 |
Số 5 |
Lần 25 |
Số 5 |
Tính xác suất thực nghiệm
Xuất hiện số 2
Một hộp có 5 chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số 1, 2, 3, 4, 5; hai thẻ khác nhau thì ghi số khác nhau. Rút ngẫu nhiên một thẻ rồi bỏ lại thẻ vào hộp.
Sau 25 lần rút thẻ liên tiếp, hãy ghi kết quả thống kê theo mẫu sau:
|
Lần 1 |
Số 3 |
Lần 6 |
Số 5 |
Lần 11 |
Số 3 |
Lần 16 |
Số 2 |
Lần 21 |
Số 1 |
|
Lần 2 |
Số 1 |
Lần 7 |
Số 2 |
Lần 12 |
Số 2 |
Lần 17 |
Số 1 |
Lần 22 |
Số 5 |
|
Lần 3 |
Số 2 |
Lần 8 |
Số 3 |
Lần 13 |
Số 2 |
Lần 18 |
Số 2 |
Lần 23 |
Số 3 |
|
Lần 4 |
Số 3 |
Lần 9 |
Số 4 |
Lần 14 |
Số 1 |
Lần 19 |
Số 3 |
Lần 24 |
Số 4 |
|
Lần 5 |
Số 4 |
Lần 10 |
Số 5 |
Lần 15 |
Số 5 |
Lần 20 |
Số 5 |
Lần 25 |
Số 5 |
Tính xác suất thực nghiệm
Xuất hiện số 1
