Cho tam giác nhọn ABC, kẻ đường cao AH, BK. Từ H kẻ HE vuông góc AB (E thuộc AB), kẻ HF vuông góc AC (F thuộc AC)
a) Chứng minh rằng:
b) Bốn điểm A, B, H, K cùng thuộc một đường tròn.
c) Cho . Tính FC
 Giải bởi Vietjack
Giải bởi Vietjack
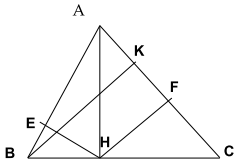
a. Áp dụng hệ thức lượng cho
+
+
+ Suy ra:
b. Gọi O là trung điểm của AB
Ta có KO là trung tuyến ứng với cạnh huyền của tam giá ABK vuông tại K nên
thuộc đường tròn đường kính AB (1)
Ta có HO là trung tuyến ứng với cạnh huyền của tam giác ABK vuông tại K nên
thuộc đường tròn đường kính AB (2)
Từ (1) và (2)đpcm
Do đó bốn điểm A, B, H, K cùng thuộc một đường tròn đường kính AB
c.
+ Trong tam giác AHC vuông tại H
Ta có:
+ Trong tam giác HFC vuông tại F, ta có:
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Cho hai số thực a; b thay đổi thoả mãn điều kiện và
Cho hàm số:
1) Tìm giá trị của m để hàm sè đồng biến trên R.
2) Khi Tính
3) Vẽ đồ thị hàm số với
Cho biểu thức với và .
a. Rút gọn các biểu thức sau:
b. Tính giá trị của P với
c. Tìm x nguyên để P có giá trị nguyên.