5 câu hỏi trắc nghiệm thuộc Đề thi Giữa kì 1 Toán lớp 9 có đáp án (Đề 4)

Đề thi Giữa kì 1 Toán lớp 9 có đáp án

Đề thi Giữa kì 1 Toán lớp 9 có đáp án (Đề 4)

3171 lượt thi
5 câu hỏi
30 phút

BẮT ĐẦU LÀM BÀI

Danh sách câu hỏi

Câu 1:

Giải các phương trình và bất phương trình sau:

a. $\frac{x + 1}{3} = x - 3$

b. $\frac{2}{x} - \frac{4}{1 - x} = \frac{3 x + 4}{x^{2} - x}$

c. $5 (x + 1) \geq 3 x + 7$

d. $\sqrt{2x + 1} = 7 - x$

Xem đáp án

a. Nghiệm của phương trình x = 5

b. Điều kiện: $x \neq 0; x \neq 1$

Phương trình cho viết thành: $\frac{2}{x} + \frac{4}{x - 1} = \frac{3 x + 4}{x (x - 1)}$

- Biến đổi về dạng: $2 x - 2 + 4 x = 3 x + 4$

- Giải ra được: $x = 2$ (thỏa mãn). Rồi kết luận

c. Giải đúng bất phương trình tìm được $x \geq 1$ . Rồi kết luận

d. Điều kiện: $- 0, 5 \leq x \leq 7$

- Giải đúng phương trình, rồi kết luận nghiệm x = 4.

Câu 2:

Cho hàm số: $y = f (x) = (m + 1) x - 2 m + 4 (m \neq - 1)$

1) Tìm giá trị của m để hàm sè đồng biến trên R.

2) Khi $m = 1 .$ Tính $f (- 1); f (2) .$

3) Vẽ đồ thị hàm số với $m = 2 .$

Xem đáp án

1. Tìm được $m \geq - 1 .$

2. Thay $m = 1$ ta được $y = f (x) = 2 x + 2$

Tính được $f (- 1) = 0; f (2) = 6$

3. Thay $m = 2$ ta được $y = f (x) = 3 x$ và vẽ đúng đồ thị

Câu 3:

Cho biểu thức $P = \frac{3}{(\sqrt{x} - 2) (\sqrt{x} + 1)} + \frac{2}{\sqrt{x} + 1} + \frac{1}{2 - \sqrt{x}}$ với $x \geq 0$ và $x \neq 4$ .

a. Rút gọn các biểu thức sau:

b. Tính giá trị của P với $x = \sqrt{48} - 2 \sqrt{75} + \sqrt{108} + 2$

c. Tìm x nguyên để P có giá trị nguyên.

Xem đáp án

- Với $x \geq 0$ và $x \neq 4$ , biến đổi:

$P = \frac{3}{(\sqrt{x} - 2) (\sqrt{x} + 1)} + \frac{2}{\sqrt{x} + 1} - \frac{1}{\sqrt{x} - 2}$

- Biến đổi đến $P = \frac{3 + 2 \sqrt{x} - 4 - \sqrt{x} - 1}{(\sqrt{x} - 2) (\sqrt{x} + 1)} = \frac{\sqrt{x} - 2}{(\sqrt{x} - 2) (\sqrt{x} + 1)} = \frac{1}{\sqrt{x} + 1}$

Vậy $P = \frac{1}{\sqrt{x} + 1}$ với $x \geq 0$ và $x \neq 4$

b. $x = \sqrt{48} - 2 \sqrt{75} + \sqrt{108} + 2 = 2$ (tmdk) $\Rightarrow P = \frac{1}{\sqrt{2} + 1} = \sqrt{2} - 1$

- Lập luận được $P = \frac{1}{\sqrt{x + 1}}$ nguyên khi $\sqrt{x} + 1$ là ước của 1

- Giải được: x = 0 (TM)

- Kết luận

Câu 4:

Cho tam giác nhọn ABC, kẻ đường cao AH, BK. Từ H kẻ HE vuông góc AB (E thuộc AB), kẻ HF vuông góc AC (F thuộc AC)

a) Chứng minh rằng: $AE . AB = AF . AC$

b) Bốn điểm A, B, H, K cùng thuộc một đường tròn.

c) Cho $\hat{HAC} = 30 °$ . Tính FC

Xem đáp án

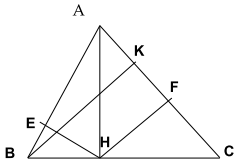
a. Áp dụng hệ thức lượng cho $∆ AHB và ∆ AHC$

+ ${AH}^{2} = AE . AB$

+ $\begin{array}{l} {AH}^{2} = AF . AC \end{array}$

+ Suy ra: $AE . AB = AF . AC$

b. Gọi O là trung điểm của AB

Ta có KO là trung tuyến ứng với cạnh huyền của tam giá ABK vuông tại K nên $OK = OA = OB$

$\Rightarrow K, A, B$ thuộc đường tròn đường kính AB (1)

Ta có HO là trung tuyến ứng với cạnh huyền của tam giác ABK vuông tại K nên $OH = OA = OB$

$\to H, A, B$ thuộc đường tròn đường kính AB (2)

$\to$ Từ (1) và (2) $\to$ đpcm

Do đó bốn điểm A, B, H, K cùng thuộc một đường tròn đường kính AB

+ Trong tam giác AHC vuông tại H

Ta có: $HC = HA . tg \hat{HAC} = 4 . tg 30 ° = 4 \frac{\sqrt{3}}{3}$

+ Trong tam giác HFC vuông tại F, ta có:

$CF = HC . \cos \hat{HCA} = \frac{4 \sqrt{3}}{3} . \cos 60 ° = \frac{4 \sqrt{3}}{3} . \frac{1}{2} = \frac{2 \sqrt{3}}{3}$

Câu 5:

Cho hai số thực a; b thay đổi thoả mãn điều kiện $a + b \geq 1$ và $1 > a > 0 .$

Tìm giá trị nhỏ nhất của biểu thức

A = \frac{8 a^{2} + b}{4 a} + b^{2}

Xem đáp án

Tìm GTNN của $A = \frac{8 a^{2} + b}{4 a} + b^{2}$ với $a + b \geq 1$ và $1 > a > 0 .$

Từ $a + b \geq 1 \Rightarrow b \geq 1 - a > 0$ ta có:

$\begin{array}{l} A= \frac{8 a^{2} + b}{4 a} + b^{2} \geq \frac{8 a^{2} + 1 - a}{4 a} + {(1 - a)}^{2} \\ = \frac{8 a^{2} - a + 1 + 4 a^{3} - 8 a^{2} + 4 a}{4 a} = \frac{4 a^{3} - 4 a^{2} + a + 4 a^{2} - 4 a + 1 + 6 a}{4 a} \\ = \frac{a {(2 a - 1)}^{2} + {(2 a - 1)}^{2}}{4 a} + \frac{3}{2} = \frac{{(2 a - 1)}^{2} (a + 1)}{4 a} + \frac{3}{2} (1) \end{array}$

Vì với $a > 0$ thì $\frac{{(2 a - 1)}^{2} (a + 1)}{4 a} \geq 0$ . Dấu bằng xảy ra khi $a = \frac{1}{2}$

Nên từ (1) suy ra: $A \geq 0 + \frac{3}{2}$ hay $A \geq \frac{3}{2} .$

Vậy GTNN của $A = \frac{3}{2}$ khi $a = b = \frac{1}{2}$

Bắt đầu thi ngay

CHỌN BỘ SÁCH BẠN MUỐN XEM

Đề thi Giữa kì 1 Toán lớp 9 có đáp án

Đề thi Giữa kì 1 Toán lớp 9 có đáp án (Đề 4)

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương