Một người dự định đi xe đạp từ A đến B cách nhau 36km trong thời gian đã định. Sau khi đi được nửa quãng đường, người đó dừng lại nghỉ 30 phút. Vì vậy mặc dù trên quãng đường còn lại đã tăng tốc thêm 2km/h song vẫn đến B chậm hơn dự kiến 12 phút. Vậy vận tốc của người đi xe đạp trên đoạn đường cuối của đoạn AB?
A. 12 km/h
B. 14 km/h
C. 10 km/h
D. 8 km/h
 Giải bởi Vietjack
Giải bởi Vietjack


Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Cho Parabol (P): y = x2 và đường thẳng (d): y =mx + 4. Biết đường thẳng (d) luôn cắt đồ thị (P) tại hai điểm phân biệt A, B. Gọi x1; x2 là hoành độ của các điểm A, B. Tìm giá trị lớn nhất của
Cho phương trình x2 – (m + 1)x – 3 = 0 (1), với x là ẩn, m là tham số. Gọi x1; x2 là hai nghiệm của phương trình (1). Đặt . Tìm m khi B đạt giá trị lớn nhất.
Cho phương trình: x2 – 2(m – 1)x + m2 − 3m = 0. Tìm m để phương trình có 2 nghiệm phân biệt x1; x2 thỏa mãn x12 + x22 = 8
Tìm m để phương trình 3x2 + 4(m – 1)x + m2 – 4m + 1 = 0 có hai nghiệm phân biệt x1; x2 thỏa mãn:
Cho parabol (P): y = x2 và đường thẳng (d): y = mx + 1. Gọi A (x1; y1) và B (x2; y2) là các giao điểm của (d) và (P). Tìm m để biểu thức M = (y1 − 1)( y2 − 1) đạt giá trị lớn nhất.
Trong mặt phẳng tọa độ Oxy, cho đường thẳng (d): 2x – y – a2 = 0 và parabol (P): y = ax2 (a > 0). Tìm a để (d) cắt (P) tại hai điểm phân biệt A, B. Khi đó có kết luận gì về vị trí của hai điểm A, B
Cho parabol (P): và đường thẳng d: . Gọi A, B là các giao điểm của (P) và d. Tìm tọa độ điểm C trên trục tung cho CA + CB có giá trị nhỏ nhất.
Tìm phương trình đường thẳng (d) đi qua điểm I (0; 1) và cắt parabol (P): y = x2 tại hai điểm phân biệt M và N sao cho MN = 2
Tìm tham số m để đường thẳng d: y = 2x + m và parabol (P): y = 2x2 không có điểm chung
Tìm các giá trị của m để đường thẳng d: y = 2(m – 1)x – m – 1 cắt parabol (P): y = x2 tại hai điểm có hoành độ trái dấu.
Trong mặt phẳng Oxy, cho parabol (P): và đường thẳng (d): x – 2y + 12 = 0. Gọi giao điểm của (d) và (P) là A, B. Tìm tọa độ điểm C nằm trên (P) sao cho tam giác ABC vuông tại C.
Trong mặt phẳng Oxy cho đường thẳng (d): y = kx và parabol (P): . Giả sử đường thẳng (d) cắt parabol (P) tại hai điểm phân biệt A, B. Tọa độ trung điểm M của đoạn thẳng AB luôn thỏa mãn phương trình nào dưới đây?
Tìm các giá trị của m để phương trình x2 – mx + m2 – m – 3 = 0 có hai nghiệm x1; x2 là độ dài các cạnh góc vuông của tam giác ABC tại A biết độ dài cạnh huyền BC = 2
Chiều cao của một tam giác vuông là 8cm chia cạnh huyền thành 2 đoạn thẳng hơn kém nhau 12cm. Tính độ dài cạnh huyền của tam giác vuông đó.
Trong mặt phẳng tọa độ Oxy, cho parabol (P) có phương trình . Gọi (d) là đường thẳng đi qua I (0; −2) và có hệ số góc k. Đường thẳng (d) cắt parabol (P) tại hai điểm phân biệt A, B. Gọi H, K theo thứ tự là hình chiếu vuông góc của A, B trên trục hoành. Khi đó tam giác IHK là tam giác?
1. Hàm số y = ax2
a) Tập xác định
Cho hàm số
Tập xác định của hàm số là R.
b) Tính chất
+ Nếu a > 0 thì hàm số nghịch biến khi x < 0 và đồng biến khi x > 0.
+ Nếu a < 0 thì hàm số đồng biến khi x < 0 và nghịch biến khi x > 0.
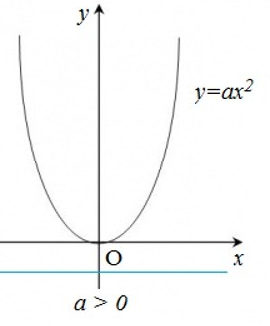
Đồ thị của hàm số là một đường cong đi qua gốc tọa độ và nhận trục Oy làm trục đối xứng. Đường cong đó được gọi là một parabol đỉnh O (với O là gốc tọa độ).
Tính chất của đồ thị:
+ Nếu a > 0 thì đồ thị nằm phía trên trục hoành, O là điểm thấp nhất của đồ thị.
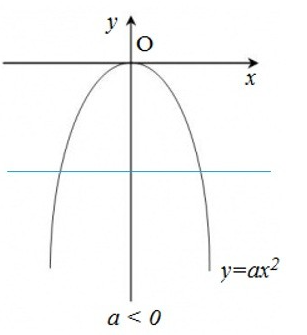
+ Nếu a < 0 thì đồ thị nằm phía dưới trục hoành, O là điểm cao nhất của đồ thị.
Bước 1: Tìm tập xác định của hàm số.
Bước 2: Lập bảng giá trị (thường từ 5 đến 7 giá trị) tương ứng giữa x và y.
Bước 3: Vẽ đồ thị và kết luận.
2. Phương trình bậc hai một ẩn
a) Định nghĩa: Phương trình bậc hai một ẩn (nói gọn là phương trình bậc hai) là phương trình có dạng
![]()
trong đó x là ẩn, a, b, c là những số cho trước gọi là các hệ số và .
b) Biệt thức
Đối với phương trình ax2 + bx + c = 0 (a ≠ 0) ta có biệt thức Δ như sau:
Δ = b2 - 4ac
Ta sửa dụng biết thức Δ để giải phương trình bậc hai.
c) Công thức nghiệm của phương trình bậc hai
Đối với phương trình ax2 + bx + c = 0 (a ≠ 0) và biệt thức Δ = b2 - 4ac
+ Nếu Δ > 0 thì phương trình có hai nghiệm phân biệt là
+ Nếu Δ = 0 thì phương trình có nghiệm kép là
+ Nếu Δ < 0 thì phương trình vô nghiệm.
d) Biệt thức
Đối với phương trình ax2 + bx + c = 0 (a ≠ 0) và b = 2b’ ta có biệt thức như sau:
= b’2 - ac
Ta sửa dụng biết thức để giải phương trình bậc hai.
e) Công thức nghiệm thu gọn của phương trình bậc hai
Đối với phương trình ax2 + bx + c = 0 (a ≠ 0) có b = 2b’ và biệt thức = b’2 - ac
+ Nếu > 0 thì phương trình có hai nghiệm phân biệt là
+ Nếu = 0 thì phương trình có nghiệm kép là
+ Nếu < 0 thì phương trình vô nghiệm.
3. Hệ thức Vi – ét
a) Hệ thức Vi – ét
Nếu x1, x2 là hai nghiệm của phương trình ax2 + bx + c = 0 (a ≠ 0) thì ta có:
b) Ứng dụng của hệ thức Vi - ét
+ Nếu phương trình ax2 + bx + c = 0 (a ≠ 0) có a + b + c = 0 thì phương trình có một nghiệm là x1 = 1 và nghiệm còn lại là
+ Nếu phương trình ax2 + bx + c = 0 (a ≠ 0) có a - b + c = 0 thì phương trình có một nghiệm là x1 = -1 và nghiệm còn lại là
+ Nếu hai số có tổng bằng S và tích bằng P thì hai số đó là nghiệm của phương trình bậc hai x2 - Sx + P = 0
+ Điều kiện để có hai số đó là S2 - 4P ≥ 0