Điền số thích hợp vào chỗ trống
Hai người khách đi du lịch xuất phát đồng thời từ hai thành phố cách nhau 40 km. Họ đi ngược chiều và gặp nhau sau 4 giờ. Hỏi vận tốc của mỗi người biết rằng đến khi gặp nhau, người thứ nhất đi nhiều hơn người thứ hai 8 km.
Đáp số: Vận tốc của người thứ nhất là … (km/h) , vận tốc của người thứ hai là … (km/h)
 Giải bởi Vietjack
Giải bởi Vietjack
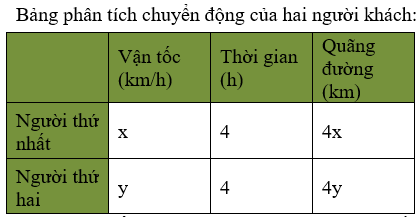
Chú ý: Chuyển động của hai người là ngược chiều nên tổng quãng đường đi được của hai người đến khi gặp nhau chính là khoảng cách giữa hai thành phố
Lời giải
Gọi vận tốc của người khách thứ nhất là x (km/h); vận tốc của người khách thứ hai là y (km/h). Điều kiện: x, y > 0
Thời gian đi được của hai người khách là 4 giờ nên ta có quãng đường đi được của người khách thứ nhất là 4x (km) và quãng đường đi được của người khách thứ hai là 4y (km)
Do hai người đi ngược chiều nhau nên khi gặp nhau, tổng quãng đường hai người khách đi được bằng với khoảng cách giữa hai thành phố
Do đó, ta có phương trình: 4x + 4y = 40 (1)
Vì khi gặp nhau, người thứ nhất đi nhiều hơn người thứ hai 8km nên ta có phương trình: 4x – 4y = 8 (2)
Từ (1) và (2), ta có hệ phương trình: {4x+4y=404x−4y=8
⇔{8x=484x−4y=8⇔{x=64y=16⇔{x=6y=4 (thỏa mãn)
Vậy vận tốc của người thứ nhất là 6 (km/h) , vận tốc của người thứ hai là 4 (km/h)
Vậy số cần điền vào chỗ trống lần lượt là 6 và 4
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Lựa chọn đáp án đúng nhất
Một khu vườn hình chữ nhật có chu vi 46m. Nếu tăng chiều dài 5m và giảm chiều rộng 3m thì chiều dài gấp 4 lần chiều rộng. Kích thước khu vườn đó là:
Lựa chọn đáp án đúng nhất
Hai năm trước đây tuổi anh gấp đôi tuổi của em, còn 8 năm trước đây, tuổi anh gấp 5 lần tuổi em. Hỏi hiện nay, anh và em bao nhiêu tuổi?
Lựa chọn đáp án đúng nhất
Hai đội trồng cây gây rừng trong tháng trước trồng được 700 cây. Trong tháng này, đội A vượt mức 60%, đội B vượt mức 40%. Tính xem mỗi đội trong tháng trước trồng được bao nhiêu cây. Biết rằng trong tháng này cả hai đội trồng được 1100 cây. Số cây mà đội A và B trồng được trong tháng trước lần lượt là:
Điền số thích hợp vào chỗ trống
Hai vòi nước cùng chảy vào một bể nước cạn thì sau 12 giờ bể đầy. Người ta mở cả hai vòi trong 4 giờ thì khóa vòi II lại và để vòi I chảy tiếp 14 giờ nữa mới đầy bể. Hỏi nếu mỗi vòi chảy riêng thì sau bao lâu mới đầy bể?
Đáp số: Thời gian vòi I chảy một mình đầy bể là … giờ. Thời gian vòi II chảy một mình đầy bể là … giờ
Lựa chọn đáp án đúng nhất
Giải hệ phương trình {(x−1)2−(x+2)2=9y(y−3)2−(y+2)2=5x
Hệ phương trình có nghiệm duy nhất là:
Điền số thích hợp vào chỗ trống
Giải hệ phương trình {x+y=7(x+2)(y+3)=xy+45.
Hệ phương trình có nghiệm duy nhất là (x; y) = (…; …)
Lựa chọn đáp án đúng nhất
Các đường thẳng 2x + 3y = 20; 3x – 5y = 11 và x + y = 9 đồng quy tại một điểm, đúng hay sai?
Điền số thích hợp vào chỗ trống
Một ca nô chạy xuôi dòng sông được 108 km rồi chạy ngược dòng 63 km hết tất cả 7 giờ. Một lần khác, ca nô này chạy xuôi dòng 81 km rồi ngược dòng 84 km cũng hết 7 giờ. Hãy tính vận tốc thật của ca nô và vận tốc dòng nước.
Đáp số: Vận tốc thực của ca nô là … km/h và vận tốc dòng nước là … km/h
Lựa chọn đáp án đúng nhất
Hệ phương trình {xy+2x=yxy+2y=xcó số nghiệm là:
Lựa chọn đáp án đúng nhất
Xét hệ phương trình {x−ay=aax+y=1với a là tham số. Tìm a để hệ phương trình có nghiệm thỏa mãn x > 0, y > 0
Xét hệ phương trình {x−ay=axa+y=1. Khẳng định nào sau đây là đúng?
Điền số thích hợp vào chỗ trống
Tìm giá trị nhỏ nhất của biểu thức
A = (x – 2y + 1)2 + (2x + y + 5)2
Đáp số: Giá trị nhỏ nhất của A là … đạt được khi (x; y) = (…; …)
Điền số thích hợp vào chỗ trống
Tìm các giá trị của a để hai hệ phương trình sau tương đương:
(I){2x+3y=83x−y=1 ;(II){ax−3y=−2x+y=3
Đáp số: a = …
Điền số thích hợp vào chỗ trống
Đa thức P(x) chia hết cho đa thức x − a khi và chỉ khi P(a) = 0.
Tìm giá trị của m và n sao cho đa thức sau đồng thời chia hết cho x + 1 và x + 3
P(x) = mx3 + (2m − 2)x2 − (3n − 5)x − 4n
Đáp số: m = … và n = …
Lựa chọn đáp án đúng nhất
Giải hệ phương trình: {1x−2+1y−1=22x−2−3y−1=−1
Hệ phương trình đã cho có nghiệm duy nhất là:
1. Phương trình bậc nhất hai ẩn
Phương trình bậc nhất hai ẩn x và y là hệ thức dạng
ax + by = c (1)
trong đó a, b, c là các số đã biết ( a≠0 hoặc b≠0)
2. Nghiệm của phương trình bậc nhất hai ẩn
- Phương trình bậc nhất hai ẩn luôn luôn có vô số nghiệm. Trong mặt phẳng tọa độ, tập nghiệm của nó được biểu diễn bởi đường thẳng ax + by = c (d).
- Nếu a≠0 và b≠0 thì (d) chính là đồ thị của hàm số bậc nhất y=−abx+cb
3. Hệ phương trình bậc nhất hai ẩn và tập nghiệm của hệ phương trình bậc nhất hai ẩn
a) Hệ phương trình bậc nhất hai ẩn
Cho hai phương trình bậc nhất hai ẩn là ax + by = c và a'x + b'y = c'. Khi đó ta có hệ phương trình:
(I){ax+by=ca'
Gọi (d) và (d') là đồ thị hàm số của 2 hàm số rút ra từ 2 phương trình bậc nhất hai ẩn của (I).
Đối với hệ phương trình (I), ta có:
Nếu (d) cắt (d') thì hệ (I) có một nghiệm duy nhất.
Nếu (d) song song với (d') thì hệ (I) vô nghiệm.
Nếu (d) trùng với (d') thì hệ (I) có vô số nghiệm.
Nếu a, a', b, b', c, c' đều khác 0 thì:
Hệ phương trình có nghiệm duy nhất ;
Hệ phương trình vô nghiệm ;
Hệ phương trình vô số nghiệm .
4. Giải hệ phương trình bậc nhất hai ẩn bằng phương pháp thế
Bước 1: Dùng quy tắc thế biến đổi hệ phương trình đã cho để được một hệ phương trình mới, trong đó có một phương trình một ẩn.
Bước 2: Giải phương trình một ẩn đó rồi suy ra nghiệm của hệ đã cho.
5. Giải hệ phương trình bằng phương pháp cộng đại số
Bước 1: Nhân hai vế của mỗi phương trình với các số thích hợp (nếu cần) sao cho với một ẩn nào đó các hệ số bằng nhau hoặc đối nhau.
Bước 2: Áp dụng quy tắc cộng (trừ) đại số để được một hệ phương trình mới, trong đó một phương trình có hệ số của một trong hai ẩn bằng 0 (tức là phương trình một ẩn).
Bước 3: Giải phương trình một ẩn vừa có rồi suy ra nghiệm hệ phương trình.
6. Giải bài toán bằng cách lập phương trình
Bước 1: Lập phương trình
- Chọn ẩn số và đặt điều kiện thích hợp cho ẩn số.
- Biểu diễn các đại lượng chưa biết theo ẩn và các đại lượng đã biết
- Lập phương trình biểu thị mối quan hệ giữa các đại lượng.
Bước 2: Giải phương trình
Bước 3: Trả lời
Kiểm tra xem trong các nghiệm của hệ phương trình, nghiệm nào thoả mãn điều kiện của ẩn, nghiệm nào không, rồi kết luận.