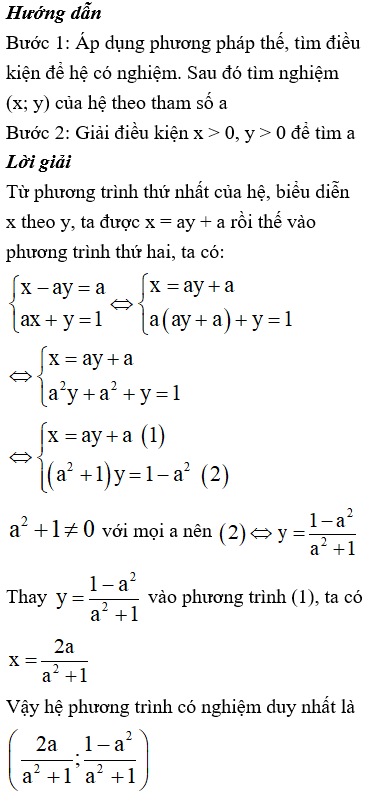20 câu hỏi trắc nghiệm thuộc Trắc nghiệm Ôn tập chương III - Đại số 9 có đáp án (Thông hiểu)

Câu 1:

Xét hệ phương trình $\{\begin{cases} x - a y = a \\ x a + y = 1 \end{cases}$ . Khẳng định nào sau đây là đúng?

A. Với a = 5, hệ phương trình có nghiệm duy nhất (5; −12)

B. Với mọi a, hệ luôn có nghiệm duy nhất

C. Với mọi $a \neq \pm 1$ , hệ có nghiệm duy nhất

Xem đáp án

Hướng dẫn

- Giải hệ phương trình với a = 5 để kiểm tra đáp án A

- Tìm điều kiện của a để hệ có nghiệm duy nhất để kiểm tra đáp án B và C

Câu 2:

Lựa chọn đáp án đúng nhất

Xét hệ phương trình $\{\begin{cases} x - a y = a \\ a x + y = 1 \end{cases}$ với a là tham số. Tìm a để hệ phương trình có nghiệm thỏa mãn x > 0, y > 0

A. a = 1

B. a > 1

C. 0 < a < 1

Xem đáp án

Câu 3:

Điền số thích hợp vào chỗ trống

Tìm các giá trị của a để hai hệ phương trình sau tương đương:

$(I) \{\begin{cases} 2 x + 3 y = 8 \\ 3 x - y = 1 \end{cases}; (I I) \{\begin{cases} a x - 3 y = - 2 \\ x + y = 3 \end{cases}$

Đáp số: a = …

Xem đáp án

Câu 4:

Điền số thích hợp vào chỗ trống

Tìm các giá trị của a, b để hai hệ phương trình sau tương đương:

$(I) \{\begin{cases} - 2 x + y = 5 \\ x + 3 y = 1 \end{cases}; (I I) \{\begin{cases} a x + b y = 2 \\ b x + y = a \end{cases}$

Đáp số: a = … và b = …

Xem đáp án

Câu 5:

Điền số thích hợp vào chỗ trống

Xác định m để hệ phương trình sau có nghiệm duy nhất:

$\{\begin{cases} 2 x - y = 1 \\ x + y = 2 \\ m x - y = 2 m \end{cases}$

Đáp số: m = …

Xem đáp án

Câu 6:

Lựa chọn đáp án đúng nhất

Giải hệ phương trình $\{\begin{cases} \frac{x + 1}{y + 2} = 5 \\ 3 (2 x - 5) - 4 (3 y + 4) = 5 \end{cases}$

Hệ phương trình có nghiệm duy nhất là:

A. (−1; 4)

B. (−4; 1)

C. (4; −1)

D. (1; −4)

Xem đáp án

Câu 7:

Điền số thích hợp vào chỗ trống

Giải hệ phương trình $\{\begin{cases} x + y = 7 \\ (x + 2) (y + 3) = x y + 45 \end{cases}$ .

Hệ phương trình có nghiệm duy nhất là (x; y) = (…; …)

Xem đáp án

Ta có:

$\{\begin{cases} x + y = 7 \\ (x + 2) (y + 3) = x y + 45 \end{cases} \Leftrightarrow \{\begin{cases} x + y = 7 \\ x y + 3 x + 2 y + 6 = x y + 45 \end{cases} \Leftrightarrow \{\begin{cases} x + y = 7 \\ 3 x + 2 y = 39 \end{cases}$

$\Leftrightarrow \{\begin{cases} x = 7 - y \\ 3 (7 - y) + 2 y = 39 \end{cases} \Leftrightarrow \{\begin{cases} x = 7 - y \\ - y = 18 \end{cases} \Leftrightarrow \{\begin{cases} x = 25 \\ y = - 18 \end{cases}$

Vậy hệ phương trình đã cho có nghiệm duy nhất là (25; −18)

Vậy số cần điền vào chỗ trống lần lượt là 25 và −18

Câu 8:

Lựa chọn đáp án đúng nhất

Giải hệ phương trình $\{\begin{cases} {(x - 1)}^{2} - {(x + 2)}^{2} = 9 y \\ {(y - 3)}^{2} - {(y + 2)}^{2} = 5 x \end{cases}$

Hệ phương trình có nghiệm duy nhất là:

A. (5; 3)

B. (−5; −3)

C. (5; −3)

D. (−5; 3)

Xem đáp án

Ta có:

$\{\begin{cases} {(x - 1)}^{2} - {(x + 2)}^{2} = 9 y \\ {(y - 3)}^{2} - {(y + 2)}^{2} = 5 x \end{cases} \Leftrightarrow \{\begin{cases} (x^{2} - 2 x + 1) - (x^{2} + 4 x + 4) = 9 y \\ (y^{2} - 6 y + 9) - (y^{2} + 4 y + 4) = 5 x \end{cases} \Leftrightarrow \{\begin{cases} 6 x + 9 y = - 3 \\ 5 x + 10 y = 5 \end{cases}$

$\Leftrightarrow \{\begin{cases} 2 x + 3 y = - 1 \\ x + 2 y = 1 \end{cases} \Leftrightarrow \{\begin{cases} 2 (1 - 2 y) + 3 y = - 1 \\ x = 1 - 2 y \end{cases} \Leftrightarrow \{\begin{cases} - y = - 3 \\ x = 1 - 2 y \end{cases} \Leftrightarrow \{\begin{cases} y = 3 \\ x = - 5 \end{cases}$

Vậy hệ phương trình đã cho có nghiệm duy nhất là (−5; 3)

Đáp án cần chọn là: D

Câu 9:

Lựa chọn đáp án đúng nhất

Giải hệ phương trình: $\{\begin{cases} \frac{1}{x - 2} + \frac{1}{y - 1} = 2 \\ \frac{2}{x - 2} - \frac{3}{y - 1} = - 1 \end{cases}$

Hệ phương trình đã cho có nghiệm duy nhất là:

A. (3; 2)

B. (2; 3)

C. (1; 2)

D. (2; 1)

Xem đáp án

Điều kiện: $x \neq 2; y \neq 1$

Đặt $u = \frac{1}{x - 2}, v = \frac{1}{y - 1}$ , ta có hệ phương trình: $\{\begin{cases} u + v = 2 \\ 2 u - 3 v = - 1 \end{cases}$

Từ phương trình thứ nhất, biểu diễn u theo v, ta được: u = 2 – v

Thế u = 2 – v vào phương trình thứ 2, ta được:

$\{\begin{cases} u = 2 - v \\ 2 (2 - v) - 3 v = - 1 \end{cases} \Leftrightarrow \{\begin{cases} u = 2 - v \\ - 5 v = - 5 \end{cases} \Leftrightarrow \{\begin{cases} u = 1 \\ v = 1 \end{cases}$

Suy ra $\{\begin{cases} \frac{1}{x - 2} = 1 \\ \frac{1}{y - 1} = 1 \end{cases} \Leftrightarrow \{\begin{cases} x - 2 = 1 \\ y - 1 = 1 \end{cases} \Leftrightarrow \{\begin{cases} x = 3 \\ y = 2 \end{cases}$ (thỏa mãn)

Vậy hệ phương trình có nghiệm duy nhất là (3; 2)

Đáp án cần chọn là: A

Câu 10:

Lựa chọn đáp án đúng nhất

Các đường thẳng 2x + 3y = 20; 3x – 5y = 11 và x + y = 9 đồng quy tại một điểm, đúng hay sai?

A. Đúng.

B. Sai.

Xem đáp án

Xét hệ phương trình: $\{\begin{cases} 2 x + 3 y = 20 (1) \\ 3 x - 5 y = 11 (2) \\ x + y = 9 (3) \end{cases}$

$(3) \Leftrightarrow x = 9 - y (*)$

Thế x = 9 – y vào (1), ta được: $2 (9 - y) + 3 y = 20 \Leftrightarrow y = 2$

Thế x = 9 – y vào (2), ta được: $3 (9 - y) - 5 y = 11 \Leftrightarrow - 8 y = - 16 \Leftrightarrow y = 2$

Như vậy, với x = 9 – y, thì phương trình (1) và (2) đều tìm được y = 2

Thay y = 2 vào (*), ta được: x = 9 – 2 = 7

Vậy hệ phương trình trên có nghiệm duy nhất là (7; 2)

Suy ra ba đường thẳng đã cho cùng đi qua điểm (7; 2) hay ba đường thẳng đồng quy tại một điểm

Đáp án cần chọn là: A

Câu 11:

Điền số thích hợp vào chỗ trống

Tìm giá trị nhỏ nhất của biểu thức

A = (x – 2y + 1)² + (2x + y + 5)²

Đáp số: Giá trị nhỏ nhất của A là … đạt được khi (x; y) = (…; …)

Xem đáp án

Câu 12:

Lựa chọn đáp án đúng nhất

Hệ phương trình $\{\begin{cases} x y + 2 x = y \\ x y + 2 y = x \end{cases}$ có số nghiệm là:

A. 0

B. 1

C. 2

D. 3

Xem đáp án

Ta có: $\{\begin{cases} x y + 2 x = y (1) \\ x y + 2 y = x (2) \end{cases}$

Trừ từng vế hai phương trình của hệ cho nhau, ta được:

$(x y + 2 x) - (x y + 2 y) = y - x \Leftrightarrow x = y$

Thay x = y vào phương trình (1) ta có:

$y^{2} + 2 y = y \Leftrightarrow y^{2} + y = 0 \Leftrightarrow y (y + 1) = 0 \Leftrightarrow [\begin{array}{l} y = 0 \\ y = - 1 \end{array}$

Suy ra $[\begin{array}{l} x = y = 0 \\ x = y = - 1 \end{array}$

Vậy hệ phương trình đã cho có hai nghiệm là (0; 0) và (−1; −1)

Đáp án cần chọn là: C

*Nhận xét:

Hệ phương trình trong bài toán trên là hệ phương trình đối xứng loại I: Khi ta thay đổi vai trò của x và y cho nhau thì hệ phương trình không thay đổi

Câu 13:

Điền số thích hợp vào chỗ trống

Đa thức P(x) chia hết cho đa thức x − a khi và chỉ khi P(a) = 0.

Tìm giá trị của m và n sao cho đa thức sau đồng thời chia hết cho x + 1 và x + 3

P(x) = mx³+ (2m − 2)x²− (3n − 5)x − 4n

Đáp số: m = … và n = …

Xem đáp án

Đa thức P(x) chia hết cho x + 1

$\begin{array}{l} \Leftrightarrow P (- 1) = 0 \Leftrightarrow - m + (2 m - 2) + (3 n - 5) - 4 n = 0 \\ \Leftrightarrow m - n = 7 (1) \end{array}$

Đa thức P(x) chia hết cho x + 3

$\begin{array}{l} \Leftrightarrow P (- 3) = 0 \Leftrightarrow - 27 m + 9 (2 m - 2) + 3 (3 n - 5) - 4 n = 0 \\ \Leftrightarrow - 9 m + 5 n = 33 (2) \end{array}$

Từ (1) và (2), ta có hệ phương trình $\{\begin{cases} m - n = 7 \\ 9 m - 5 n = - 33 \end{cases}$

$\{\begin{cases} m = n + 7 \\ 9 (n + 7) - 5 n = - 33 \end{cases} \Leftrightarrow \{\begin{cases} m = n + 7 \\ 4 n = - 96 \end{cases} \Leftrightarrow \{\begin{cases} m = - 17 \\ n = - 24 \end{cases}$

Vậy m = −17, n = −24 thì thỏa mãn yêu cầu đề bài

Vậy số cần điền vào chỗ trống lần lượt là −17; −14

Câu 14:

Lựa chọn đáp án đúng nhất

Một khu vườn hình chữ nhật có chu vi 46m. Nếu tăng chiều dài 5m và giảm chiều rộng 3m thì chiều dài gấp 4 lần chiều rộng. Kích thước khu vườn đó là:

A. 8m và 15m

B. 7m và 16m

C. 9m và 14m

D. 6m và 17m

Xem đáp án

Hướng dẫn

Bước 1: Lập hệ phương trình

+ Gọi ẩn là các kích thước của khu vườn

+ Lập phương trình biểu thị chu vi của hình chữ nhật

+ Lập phương trình biểu thị kích thước chiều dài và chiều rộng từ giả thiết thứ hai

Bước 2: Giải hệ phương trình vừa lập

Bước 3: Kiểm tra và kết luận bài toán

Lời giải

Gọi chiều dài khu vườn là x (m); chiều rộng khu vườn là y (m).

Điều kiện: x > y > 0

Vì chu vi khu vườn là 46m, nên ta có phương trình:

2 (x + y) = 46 hay x + y = 23 (1)

Tăng chiều dài 5m thì chiều dài là x + 5 (m) và giảm chiều rộng 3m thì chiều rộng là y – 3 (m)

Do chiều dài gấp 4 lần chiều rộng nên ta có phương trình:

x + 5 = 4 (y – 3) hay x – 4y = −17 (2)

Từ (1) và (2), ta có hệ phương trình $\{\begin{cases} x + y = 23 \\ x - 4 y = - 17 \end{cases}$

$\Leftrightarrow \{\begin{cases} 5 y = 40 \\ x - 4 y = - 17 \end{cases} \Leftrightarrow \{\begin{cases} y = 8 \\ x = 4 y - 17 \end{cases} \Leftrightarrow \{\begin{cases} y = 8 \\ x = 15 \end{cases}$ (thỏa mãn)

Vậy chiều dài khu vườn là 15m và chiều rộng là 8m

Đáp án cần chọn là: A

Câu 15:

Lựa chọn đáp án đúng nhất

Hai đội trồng cây gây rừng trong tháng trước trồng được 700 cây. Trong tháng này, đội A vượt mức 60%, đội B vượt mức 40%. Tính xem mỗi đội trong tháng trước trồng được bao nhiêu cây. Biết rằng trong tháng này cả hai đội trồng được 1100 cây. Số cây mà đội A và B trồng được trong tháng trước lần lượt là:

A. 100 cây và 600 cây

B. 600 cây và 100 cây

C. 500 cây và 200 cây

Xem đáp án

Câu 16:

Điền số thích hợp vào chỗ trống

Một ca nô chạy xuôi dòng sông được 108 km rồi chạy ngược dòng 63 km hết tất cả 7 giờ. Một lần khác, ca nô này chạy xuôi dòng 81 km rồi ngược dòng 84 km cũng hết 7 giờ. Hãy tính vận tốc thật của ca nô và vận tốc dòng nước.

Đáp số: Vận tốc thực của ca nô là … km/h và vận tốc dòng nước là … km/h

Xem đáp án

Hướng dẫn

Bước 1: Lập hệ phương trình

+ Gọi ẩn là vận tốc thực của ca nô và vận tốc dòng nước. Xác định vận tốc của ca nô khu xuôi dòng và ngược dòng

+ Lập phương trình biểu thị thời gian của ca nô với từng giả thiết bài toán

Bước 2: Giải hệ phương trình vừa lập bằng phương pháp đặt ẩn phụ

Bước 3: Kiểm tra nghiệm và kết luận

Lời giải

Gọi vận tốc ca nô là x (km/h), vận tốc dòng nước là y (km/h).

Điều kiện: x > y > 0

Vận tốc xuôi dòng của ca nô là x + y (km/h); vận tốc ngược dòng của ca nô là x – y (km/h)

Một ca nô xuôi dòng một dòng sông dài 108km hết $\frac{108}{x + y}$ giờ và sau đó ngược dòng 63km hết $\frac{63}{x - y}$ giờ.

Vì tổng thời gian hết 7 giờ nên ta có phương trình:

$\frac{108}{x + y} + \frac{63}{x - y} = 7 (1)$

Ca nô xuôi dòng 81km hết $\frac{81}{x + y}$ giờ và sau đó ngược dòng 84km hết $\frac{84}{x - y}$ giờ. Vì tổng thời gian hết 7 giờ nên ta có phương trình:

$\frac{81}{x + y} + \frac{84}{x - y} = 7 (2)$

Từ (1) và (2), ta có hệ phương trình: $\{\begin{cases} \frac{108}{x + y} + \frac{63}{x - y} = 7 \\ \frac{81}{x + y} + \frac{84}{x - y} = 7 \end{cases}$

Đặt $\frac{1}{x + y} = u; \frac{1}{x - y = v}$

Ta có phương trình: $\{\begin{cases} 108 u + 63 v = 7 \\ 81 u + 84 v = 7 \end{cases}$

Giải hệ ta tìm được $u = \frac{1}{27}; v = \frac{1}{21}$

Suy ra $\{\begin{cases} x + y = 27 \\ x - y = 21 \end{cases} \Leftrightarrow \{\begin{cases} 2 x = 48 \\ y = x - 21 \end{cases} \Leftrightarrow \{\begin{cases} x = 24 \\ y = 3 \end{cases}$ (thỏa mãn)

Vậy vận tốc thực của ca nô là 24km.h và vận tốc dòng nước là 3km/h

Vậy số cần điền vào chỗ trống lần lượt là 24 và 3

Câu 17:

Sắp xếp các câu để được Lời giải đúng

Dung dịch thứ nhất chứa 30% axit HCl, dung dịch thứ hai chưa 55% axit HCl. Hỏi phải trộn bao nhiêu lít dung dịch loại thứ nhất với dung dịch loại thứ hai để được 100 lít dung dịch chứa 50% axit HCl.

1. Lượng axit HCl có trong dung dịch thứ nhất là 30%x (lít). Lượng axit HCl có trong dung dịch thứ hai là 55%y (lít). Lượng axit HCl có trong 100 lít dung dịch chứa 50% axit HCl là 50%. 100 = 50 (lít). Theo đề ra, ta có phương trình:

30%x + 55%y = 50 (1)

2. Vậy cần trộn 20 lít dung dịch loại thứ nhất với 80 lít dung dịch loại thứ hai để được 100 lít dung dịch chứa 50% axit HCl

3. Gọi x là số lít dung dịch loại thứ nhất và y là số lít dung dịch loại thứ hai cần trộn để được 100 lít dung dịch chứa 50% axit HCl. Điều kiện: 0 < x, y < 100

4. Giải hệ phương trình, ta tìm được x = 20 và y = 80 (thỏa mãn)

5. Từ (1) và (2), ta có hệ phương trình: $\{\begin{cases} x + y = 100 \\ 30 % x + 55 % y = 50 \end{cases}$

6. Do tổng số lít là 100 nên ta có phương trình x + y = 100 (2)

Xem đáp án

Ta sắp xếp theo trình tự giải sau:

Gọi x là số lít dung dịch loại thứ nhất và y là số lít dung dịch loại thứ hai cần trộn để được 100 lít dung dịch chứa 50% axit HCl. Điều kiện: 0 < x, y < 100

Lượng axit HCl có trong dung dịch thứ nhất là 30%x (lít).

Lượng axit HCl có trong dung dịch thứ hai là 55%y (lít).

Lượng axit HCl có trong 100 lít dung dịch chứa 50% axit HCl là 50%. 100 = 50 (lít).

Theo đề ra, ta có phương trình:

30%x + 55%y = 50 (1)

Do tổng số lít là 100 nên ta có phương trình x + y = 100 (2)

Từ (1) và (2), ta có hệ phương trình: $\{\begin{cases} x + y = 100 \\ 30 % x + 55 % y = 50 \end{cases}$

$\Leftrightarrow \{\begin{cases} x + y = 100 \\ \frac{30}{100} x + \frac{55}{100} y = 50 \end{cases} \Leftrightarrow \{\begin{cases} x + y = 100 \\ 6 x + 11 y = 1000 \end{cases} \Leftrightarrow \{\begin{cases} x = 100 - y \\ 6 (100 - y) + 11 y = 1000 \end{cases}$

$\Leftrightarrow \{\begin{cases} x = 100 - y \\ 5 y = 400 \end{cases} \Leftrightarrow \{\begin{cases} x = 100 - y \\ y = 80 \end{cases} \Leftrightarrow \{\begin{cases} x = 20 \\ y = 80 \end{cases}$ (thỏa mãn)

Vậy cần trộn 20 lít dung dịch loại thứ nhất với 80 lít dung dịch loại thứ hai để được 100 lít dung dịch chứa 50% axit HCl

Câu 18:

Điền số thích hợp vào chỗ trống

Hai vòi nước cùng chảy vào một bể nước cạn thì sau 12 giờ bể đầy. Người ta mở cả hai vòi trong 4 giờ thì khóa vòi II lại và để vòi I chảy tiếp 14 giờ nữa mới đầy bể. Hỏi nếu mỗi vòi chảy riêng thì sau bao lâu mới đầy bể?

Đáp số: Thời gian vòi I chảy một mình đầy bể là … giờ. Thời gian vòi II chảy một mình đầy bể là … giờ

Xem đáp án

Hướng dẫn

Bước 1: Lập hệ phương trình

+ Gọi ẩn là thời gian mỗi vòi chảy một mình đầy bể

+ Từ giả thiết hai vòi cùng chảy thì sau 12 giờ đầy bể, ta thiết lập phương trình biểu thị trong 1 giờ, số phần bể hai vòi chảy được

+ Từ giả thiết thứ hai, ta tính xem từ lúc khóa vòi II thì vòi I chảy được bao nhiêu phần bể rồi từ đó thiết lập phương trình

Bước 2: Giải hệ phương trình vừa lập

Bước 3: Kiểm tra nghiệm có thỏa mãn điều kiện không và kết luận bài toán

Lời giải

Gọi x giờ là thời gian vòi I chảy một mình đầy bể; y giờ là thời gian vòi II chảy một mình đầy bể

Điều kiện: x > 0, y > 0

Trong 1 giờ vòi I chảy được $\frac{1}{x}$ bể, vòi II chảy được $\frac{1}{y}$ bể

Do hai vòi chảy 12 giờ thì đầy bể nên trong 1 giờ, hai vòi chảy được $\frac{1}{12}$ bể nên ta có phương trình:

$\frac{1}{x} + \frac{1}{y} = \frac{1}{12} (2)$

Hai vòi chảy trong 4 giờ thì được $\frac{4}{12} = \frac{1}{3}$ bể. Sau đó khóa vòi II và vòi I chảy tiếp trong 14 giờ nữa mới đầy bể nên vòi I chảy thêm $\frac{14}{x}$ phần bể

Vì số phần bể còn lại sau khi khóa vòi II là $1 - \frac{1}{3} = \frac{2}{3}$ nên ta có phương trình:

$\frac{14}{x} = \frac{2}{3} (2)$

Từ (1) và (2), ta có hệ phương trình: $\{\begin{cases} \frac{1}{x} + \frac{1}{y} = \frac{1}{12} \\ \frac{14}{x} = \frac{2}{3} \end{cases}$

$\Leftrightarrow \{\begin{cases} \frac{1}{x} + \frac{1}{y} = \frac{1}{12} \\ x = 21 \end{cases} \Leftrightarrow \{\begin{cases} \frac{1}{21} + \frac{1}{y} = \frac{1}{12} \\ x = 21 \end{cases} \Leftrightarrow \{\begin{cases} x = 21 \\ y = 28 \end{cases}$ (thỏa mãn)

Vậy vòi I chảy một mình đầy bể trong 21 giờ, vòi II chảy một mình đầy bể trong 28 giờ.

Vậy số cần điền vào chỗ trống lần lượt là 21 và 28.

Câu 19:

Lựa chọn đáp án đúng nhất

Hai năm trước đây tuổi anh gấp đôi tuổi của em, còn 8 năm trước đây, tuổi anh gấp 5 lần tuổi em. Hỏi hiện nay, anh và em bao nhiêu tuổi?

A. Hiện nay, em 12 tuổi, anh 18 tuổi

B. Hiện nay, em 12 tuổi, anh 17 tuổi

C. Hiện nay, em 11 tuổi, anh 18 tuổi

D. Hiện nay, em 10 tuổi, anh 18 tuổi

Xem đáp án

Hướng dẫn

Lập hệ phương trình:

+ Chọn ẩn là tuổi anh và tuổi em hiện nay. Đặt điều kiện cho ẩn.

+ Thiết lập phương trình biểu thị cho tuổi anh và tuổi em hai năm trước

+ Thiết lập biểu thức tuổi anh và em hai năm sau.

Lời giải

Gọi tuổi anh hiện nay là x (tuổi), tuổi em hiện nay là y (tuổi)

Điều kiện: x > y > 8

Hai năm trước, tuổi anh là x – 2 (tuổi), tuổi em là y – 2 (tuổi)

Vì hai năm trước đây, tuổi anh gấp đôi tuổi em nên ta có phương trình:

x – 2 = 2 (y – 2) (1)

Tám năm trước, tuổi anh là x – 8 (tuổi), tuổi em là y – 8 (tuổi)

Vì 8 năm trước đây, tuổi anh gấp 5 lần tuổi em nên ta có phương trình:

x – 8 = 5 (y – 8) (2)

Từ (1) và (2), ta có hệ phương trình $\{\begin{cases} x - 2 = 2 (y - 2) \\ x - 8 = 5 (y - 8) \end{cases}$

$\Leftrightarrow \{\begin{cases} x - 2 y = - 2 \\ x - 5 y = - 32 \end{cases} \Leftrightarrow \{\begin{cases} 3 y = 30 \\ x - 5 y = - 32 \end{cases} \Leftrightarrow \{\begin{cases} y = 10 \\ x = 18 \end{cases}$ (thỏa mãn)

Vậy hiện nay, anh 18 tuổi, em 10 tuổi

Đáp án cần chọn là: D

Câu 20:

Điền số thích hợp vào chỗ trống

Hai người khách đi du lịch xuất phát đồng thời từ hai thành phố cách nhau 40 km. Họ đi ngược chiều và gặp nhau sau 4 giờ. Hỏi vận tốc của mỗi người biết rằng đến khi gặp nhau, người thứ nhất đi nhiều hơn người thứ hai 8 km.

Đáp số: Vận tốc của người thứ nhất là … (km/h) , vận tốc của người thứ hai là … (km/h)

Xem đáp án

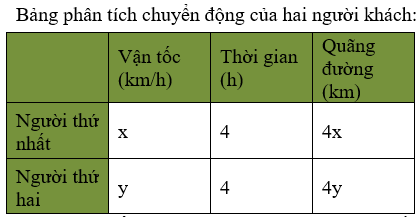
Chú ý: Chuyển động của hai người là ngược chiều nên tổng quãng đường đi được của hai người đến khi gặp nhau chính là khoảng cách giữa hai thành phố

Lời giải

Gọi vận tốc của người khách thứ nhất là x (km/h); vận tốc của người khách thứ hai là y (km/h). Điều kiện: x, y > 0

Thời gian đi được của hai người khách là 4 giờ nên ta có quãng đường đi được của người khách thứ nhất là 4x (km) và quãng đường đi được của người khách thứ hai là 4y (km)

Do hai người đi ngược chiều nhau nên khi gặp nhau, tổng quãng đường hai người khách đi được bằng với khoảng cách giữa hai thành phố

Do đó, ta có phương trình: 4x + 4y = 40 (1)

Vì khi gặp nhau, người thứ nhất đi nhiều hơn người thứ hai 8km nên ta có phương trình: 4x – 4y = 8 (2)

Từ (1) và (2), ta có hệ phương trình: $\{\begin{cases} 4 x + 4 y = 40 \\ 4 x - 4 y = 8 \end{cases}$

$\Leftrightarrow \{\begin{cases} 8 x = 48 \\ 4 x - 4 y = 8 \end{cases} \Leftrightarrow \{\begin{cases} x = 6 \\ 4 y = 16 \end{cases} \Leftrightarrow \{\begin{cases} x = 6 \\ y = 4 \end{cases}$ (thỏa mãn)

Vậy vận tốc của người thứ nhất là 6 (km/h) , vận tốc của người thứ hai là 4 (km/h)

Vậy số cần điền vào chỗ trống lần lượt là 6 và 4

CHỌN BỘ SÁCH BẠN MUỐN XEM

Trắc nghiệm Ôn tập chương III - Đại số 9 có đáp án

Trắc nghiệm Ôn tập chương III - Đại số 9 có đáp án (Thông hiểu)

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương