Cho tam giác ABC có đáy BC = 30cm, chiều cao AH = 20cm. Một đường thẳng song song với BC cánh BC là 5cm cắt các cạnh AB, AC lần lượt tại D, E. Tính diện tích tam giác ADE
 Giải bởi Vietjack
Giải bởi Vietjack


Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Cho hình vuông ABCD, M là một điểm tùy ý trên đường chéo BD. Kẻ ME ^ AB; MF ^ AD.
a) Chứng minh: DE = CF;
b) Chứng minh DE ^ FC;
c) Xác định vị trí của điểm M để diện tích tứ giác AMEF lớn nhất
Cho tam giác ABC. Trên cạnh AB lấy một điểm E sao cho BE = 3EA. Trên cạnh BC lấy một điểm F sao cho BF = 4FC. Gọi D là giao điểm của AF và CE.
a) Chứng minh SACF = SAEF.
b) Từ E và C kẻ EH, CK vuông góc với AF. Chứng minh EH = CK.
c) Chứng minh CD = DE.
d) Chứng minh SABC = 2SABD
Cho hình chữ nhật ABCD có AB = 10cm, BC = 6cm. Trên các cạnh AB, AD lần lượt lấy M, N sao cho AM = AN = x.
a) Tính diện tích đa giác MBCDN theo x
Cho hình vuông ABCD cạnh 12cm. Các điểm M, N lần lượt trên các cạnh AB, AD sao cho AM = DN = x.
a) Tính diện tích tam giác AMN theo x.
b) Tìm x để diện tích tam giác AMN bằng diện tích hình vuông ABCD
Cho tam giác ABC và điểm M nằm trong tam giác. Các đường thẳng AM, BM, CM cắt cạnh đối diện của tam giác ABC tại D, E, F. Chứng minh
Cho tam giác ABC vuông tại A và điểm H di chuyển trên BC. Gọi E, F lần lượt là điểm đối xứng của H qua AB, AC.
a) Chứng minh A, E, F thẳng hàng.
b) Chứng minh BEFC là hình thang. Có thể tìm được vị trí của H để BEFC là hình bình hành, hình chữ nhật không?
c) Xác định vị trí của H để tam giác EHF có diện tích lớn nhất
Cho tam giác ABC vuông tại A. AB = 7,5 cm; BC = 12,5 cm.
a) Tính diện tích tam giác ABC.
b) Lấy điểm M trên cạnh AB sao cho AM : MB = 1 : 2. Từ M kẻ đường thẳng song song với BC cắt trung tuyến AF tại E và cắt cạnh AC tại N. Chứng minh E là trung điểm của MN.
c) Gọi G, H lần lượt là trung điểm của MC, BN. Chứng minh EGFH là hình chữ nhật và tính diện tích của nó.
Cho G là trọng tâm của tam giác ABC. Gọi M là giao điểm của BG và AC. Chứng minh:
a) SGBC = SMBC.
b) SGBC = SGAC = SGAB
Cho tam giác ABC cân tại A, đường cao AM. Các đường trung tuyến BD, CE cắt nhau tại G. H, K thứ tự là trung điểm của BG, CG.
a) Tứ giác EHKD là hình gì? Vì sao?
b) Cho SABC = S36cm2. Tính SEHKD
Cho hình bình hành ABCD. Gọi P, Q, R, G thứ tự là điểm thuộc AB, BC, CD, DA sao cho
Các đoạn AQ và CG cắt BR và DP theo thứ tự tại I, K, M, N.
Chứng minh:
a) Tứ giác IKMN là hình gì ?
b) PR và QG cắt nhau ở trung điểm mỗi đường.
c) DBCR và DCDG có diện tích bằng nhau.
a) Cho tứ giác ABCD có AC ^ BD, AC = 6cm, SABCD = 15cm2. Tính độ dài đường chéo BD.
b) Cho tứ giác ABCD. Chứng minh SABCD ≤ 0.5.AC.BD
Cho tam giác ABC, gọi D là điểm trên cạnh AC ( AD < AC). Hãy vẽ đường thẳng qua D cắt BC ở N và chia tam giác ABC thành hai phần mà diện tích DDNC bằng diện tích DABC
Cho tam giác ABC. Các đường cao AD, BE, CK cắt nhau tại H. Chứng minh:
1. Khái niệm về đa giác
Định nghĩa: Đa giác lồi là đa giác luôn nằm trong một nửa mặt phẳng mà bờ là đường thẳng chứa bất kì cạnh nào của đa giác đó.
• Đa giác ABCDE là hình gồm năm đoạn thẳng AB, BC, CD, DE, EA, trong đó bất kì hai đoạn thẳng nào có một điểm chung cũng không cùng nằm trên một đường thẳng AB, BC, CD, DE, EA được gọi là các cạnh của đa giác đó.
Khi đó, đa giác ABCDE là đa giác lồi.
Chú ý: Từ nay nếu nhắc đến đa giác thì ta quy ước đó là đa giác lồi.
2. Đa giác đều
Đa giác đều là đa giác có tất cả các cạnh bằng nhau và tất cả các góc bằng nhau.
3. Khái niệm diện tích đa giác
• Số đo của một phần mặt phẳng giới hạn bởi một đa giác được gọi là diện tích đa giác đó.
• Mỗi đa giác có một diện tích xác định. Diện tích đa giác là một số dương.
Diện tích đa giác có các tính chất sau:
• Hai tam giác bằng nhau thì có diện tích bằng nhau.
• Nếu một đa giác được chia thành những đa giác không có điểm trong chung thì diện tích của nó bằng tổng diện tích của những đa giác đó.
4. Công thức diện tích hình chữ nhật
Diện tích hình chữ nhật là tích hai kích thức của nó: S = a . b
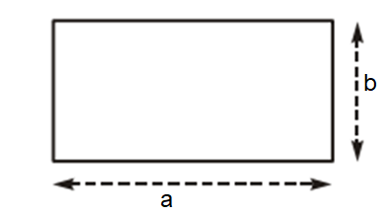
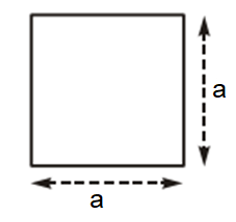
5. Công thức diện tích hình vuông, diện tích tam giác vuông
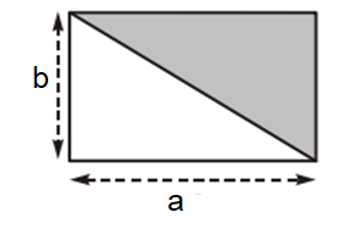
Diện tích hình vuông bằng bình phương cạnh của nó: S = .
Diện tích tam giác vuông bằng nửa tích hai cạnh góc vuông: S = a.b.
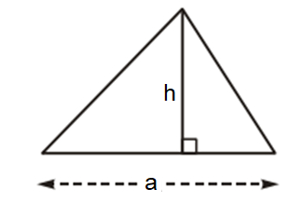
5. Công thức diện tích tam giác
Diện tích tam giác bằng nửa tích của một cạnh với chiều cao ứng với cạnh đó.
S = a . h.
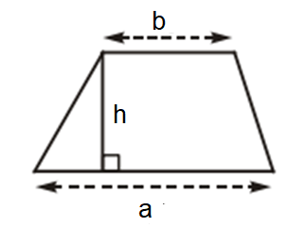
6. Công thức diện tích của hình thang
Diện tích hình thang bằng một nửa tích của tổng hai đáy với chiều cao.
S = (a + b) . h
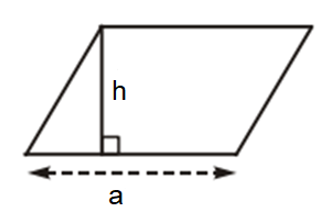
7. Công thức tính diện tích hình bình hành
Diện tích hình bình hành bằng tích của một cạnh với chiều cao tương ứng với cạnh đó: S = a . h
8. Diện tích tứ giác có hai đường chéo vuông góc
Diện tích của một tứ giác có hai đường chéo vuông góc bằng nửa tích độ dài hai đường chéo đó.
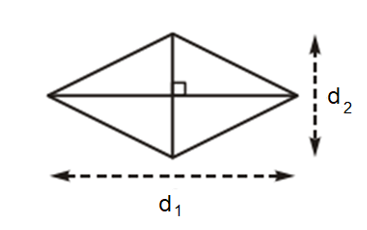
9. Công thức tính diện tích hình thoi
Diện tích hình thoi bằng nửa tích hai đường chéo.
S = d1 . d2
10. Cách tính diện tích đa giác
• Với một đa giác bất kì không có công thức tính. Cụ thể, ta có thể thực hiện các cách sau để tính diện tích đa giác:
+ Chia đa giác đó thành các tam giác riêng biệt rồi tính diện tích từng tam giác sau đó cộng các kết quả lại với nhau.
+ Tạo ra một tam giác chứa đa giác đó rồi tính diện tích đa giác bằng cách lấy tam giác lớn trừ đi diện tích của các “phần thừa”.
• Với một số hình đặc biệt ta có thể chia đa giác thành nhiều phần, mỗi phần đều là những hình mà ta dễ tính diện tích như: hình thang vuông, hình thoi, hình chữ nhật, hình vuông,...