16 câu hỏi trắc nghiệm thuộc Bài tập: Ôn tập chương II (đề số 1)

Câu 1:

Tính số đường chéo của một đa giác có 7 cạnh.

Xem đáp án

Số đường chéo đa giác có 7 cạnh là: $\frac{7. (7 - 3)}{2} = 14$

Công thức tổng quát tính số đường chéo đa giác: $\frac{n . (n - 3)}{2}$

Câu 2:

Tính số cạnh của một đa giác đều có tổng góc trong bằng 1440⁰

Xem đáp án

Gọi n là số cạnh đa giác: 180⁰. (n - 2) = 1440⁰ Þ n = 10

Công thức tổng quát tổng số đo các góc trong đa giác: 180⁰. (n - 2)

Câu 3:

Cho hình vuông ABCD cạnh 12cm. Các điểm M, N lần lượt trên các cạnh AB, AD sao cho AM = DN = x.

a) Tính diện tích tam giác AMN theo x.

b) Tìm x để diện tích tam giác AMN bằng $\frac{1}{9}$ diện tích hình vuông ABCD

Xem đáp án

Câu 4:

Cho hình chữ nhật ABCD có AB = 10cm, BC = 6cm. Trên các cạnh AB, AD lần lượt lấy M, N sao cho AM = AN = x.

a) Tính diện tích đa giác MBCDN theo x

Xem đáp án

Tương tự bài 2A ta có $S_{M B C D N} = S_{A B C D} - S_{A M N} = 60 - \frac{1}{2} (10 - x) . (6 - x)$

Câu 5:

Cho tam giác ABC. Trên cạnh AB lấy một điểm E sao cho BE = 3EA. Trên cạnh BC lấy một điểm F sao cho BF = 4FC. Gọi D là giao điểm của AF và CE.

a) Chứng minh S_ACF = S_AEF.

b) Từ E và C kẻ EH, CK vuông góc với AF. Chứng minh EH = CK.

c) Chứng minh CD = DE.

d) Chứng minh S_ABC = 2S_ABD

Xem đáp án

a) Ta chứng minh:

$S_{A E F} = S_{A B C D} = \frac{1}{4} S_{A B F}$

b) Từ câu a suy ra EH = CK

c) Gọi S_BDE = S₁; S_ADE = S₂;

Ta chứng minh DE = DC;

Ta tính được:

A_BDC = S₁; S_ADC = S₂, suy ra S_ABC = 2(S₁ + S₂) = 2.S_ABD

Câu 6:

Cho G là trọng tâm của tam giác ABC. Gọi M là giao điểm của BG và AC. Chứng minh:

a) S_GBC = $\frac{2}{3}$ S_MBC.

b) S_GBC = S_GAC = S_GAB

Xem đáp án

Câu 7:

Cho tam giác ABC cân tại A, đường cao AM. Các đường trung tuyến BD, CE cắt nhau tại G. H, K thứ tự là trung điểm của BG, CG.

a) Tứ giác EHKD là hình gì? Vì sao?

b) Cho S_ABC = S36cm². Tính S_EHKD

Xem đáp án

Câu 8:

Cho tam giác ABC có đáy BC = 30cm, chiều cao AH = 20cm. Một đường thẳng song song với BC cánh BC là 5cm cắt các cạnh AB, AC lần lượt tại D, E. Tính diện tích tam giác ADE

Xem đáp án

Câu 9:

Cho tam giác ABC. Các đường cao AD, BE, CK cắt nhau tại H. Chứng minh: $\frac{H D}{A D} + \frac{H E}{B E} + \frac{H K}{C K} = 1.$

Xem đáp án

Ta có

$\frac{S_{H B C}}{S_{A B C}} = \frac{H D}{A D}; \frac{S_{A H C}}{S_{A B C}} = \frac{H E}{B E}; \frac{S_{A H B}}{S_{A B C}} = \frac{H K}{C K} \Rightarrow \frac{H D}{A D} + \frac{H E}{B E} + \frac{H K}{C K} = \frac{S_{H B C}}{S_{A B C}} + \frac{S_{A H C}}{S_{A B C}} + \frac{S_{A H B}}{S_{A B C}} = 1.$

Câu 10:

Cho tam giác ABC và điểm M nằm trong tam giác. Các đường thẳng AM, BM, CM cắt cạnh đối diện của tam giác ABC tại D, E, F. Chứng minh $\frac{A M}{A D} + \frac{B M}{B E} + \frac{C M}{C F} = 2.$

Xem đáp án

Câu 11:

Cho tam giác ABC vuông tại A và điểm H di chuyển trên BC. Gọi E, F lần lượt là điểm đối xứng của H qua AB, AC.

a) Chứng minh A, E, F thẳng hàng.

b) Chứng minh BEFC là hình thang. Có thể tìm được vị trí của H để BEFC là hình bình hành, hình chữ nhật không?

c) Xác định vị trí của H để tam giác EHF có diện tích lớn nhất

Xem đáp án

a) Chứng minh $\hat{H A B} = \hat{E A B}; \hat{H A C} = \hat{F A C} \Rightarrow \hat{E A F} = 180^{0}$

B) Chứng minh: $\hat{E B C} + \hat{F C B} = 2 (\hat{A B C} + \hat{A C B})$

= 180⁰ Þ EB//FC.

Hay EBCF là hình thang. Nếu EBCF là hình thang vuông thì AH vuông BC. Nếu EBCF là hình bình hành thì H là trung điểm BC.

Câu 12:

Cho hình vuông ABCD, M là một điểm tùy ý trên đường chéo BD. Kẻ ME ^ AB; MF ^ AD.

a) Chứng minh: DE = CF;

b) Chứng minh DE ^ FC;

c) Xác định vị trí của điểm M để diện tích tứ giác AMEF lớn nhất

Xem đáp án

a) Chứng minh AE = PM = DF ÞDAED = DDFC Þ ĐPCM;

b) Từ câu a chứng minh được DE ^ FC.

c) Gọi cạnh hình vuông a. Chu vi hình chữ nhật AEMF = 2a;

Þ ME + MF = a không đổi;

$\Rightarrow S_{A E M F} = M E . M F \leq {(\frac{M E + M F}{2})}^{2} = \frac{a^{2}}{4}$

Vậy lớn nhất khi ME = MF hay M là trung điểm BD

Câu 13:

Cho tam giác ABC vuông tại A. AB = 7,5 cm; BC = 12,5 cm.

a) Tính diện tích tam giác ABC.

b) Lấy điểm M trên cạnh AB sao cho AM : MB = 1 : 2. Từ M kẻ đường thẳng song song với BC cắt trung tuyến AF tại E và cắt cạnh AC tại N. Chứng minh E là trung điểm của MN.

c) Gọi G, H lần lượt là trung điểm của MC, BN. Chứng minh EGFH là hình chữ nhật và tính diện tích của nó.

Xem đáp án

a) Học sinh tự làm

b) Chứng minh $A N \frac{1}{2} N C \Rightarrow S_{A M E} = S_{A E N} \Rightarrow E M = E N$

hay E là trung điểm MN.

c) Chứng minh được EG//HF và HE/FG nên EHFG là hình bình hành; Mặt khác BM ^ NC (do AB ^ AC)

Suy ra EHFG là hình chữ nhật

Câu 14:

Cho hình bình hành ABCD. Gọi P, Q, R, G thứ tự là điểm thuộc AB, BC, CD, DA sao cho $\frac{A P}{A B} = \frac{B Q}{B C} = \frac{C R}{C D} = \frac{D G}{D A} = \frac{1}{3} .$

Các đoạn AQ và CG cắt BR và DP theo thứ tự tại I, K, M, N.

Chứng minh:

a) Tứ giác IKMN là hình gì ?

b) PR và QG cắt nhau ở trung điểm mỗi đường.

c) DBCR và DCDG có diện tích bằng nhau.

Xem đáp án

a) Gợi ý: Chứng minh QCGA và CRDP là hình bình hành;

b) Chứng minh DQCM = DGAB để suy ra QRGP là hình bình hành;

c) Có

$S_{R C B} = \frac{1}{3} . S_{B C D} = \frac{1}{6} . S_{A B C D}$

Và

$S_{C G D} = \frac{1}{3} . S_{A C D} = \frac{1}{6} . S_{A B C D}$ Þ ĐPCM.

Câu 15:

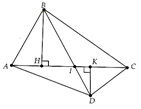
a) Cho tứ giác ABCD có AC ^ BD, AC = 6cm, S_ABCD = 15cm². Tính độ dài đường chéo BD.

b) Cho tứ giác ABCD. Chứng minh S_ABCD ≤ 0.5.AC.BD

Xem đáp án

a) HS tự làm

b) Gọi AC Ç BD = I

Kẻ BH ^ AC; DK ^ AC

Ta có BH ≤ BI; DK ≤ DI

Þ BH + DK ≤ BD

$\Rightarrow S_{A B C D} = S_{A B C} + S_{A D C} \leq \frac{1}{2} A C . B D$

Câu 16:

Cho tam giác ABC, gọi D là điểm trên cạnh AC ( AD < AC). Hãy vẽ đường thẳng qua D cắt BC ở N và chia tam giác ABC thành hai phần mà diện tích DDNC bằng $\frac{1}{3}$ diện tích DABC

Xem đáp án

Nối BD. Kẻ AM//BD

Þ S_ABD = S_MBD hay

Þ S_D_ABC = S_DMC. Gọi N là điểm trên cạnh MC mà $\frac{N C}{M C} = \frac{1}{3}$

Ta có: $S_{Δ D N C} = \frac{1}{3} S_{D M N} = \frac{1}{3} S_{A B C}$ ;

Vậy DN là đường thẳng cần tìm

CHỌN BỘ SÁCH BẠN MUỐN XEM

Bài tập: Ôn tập chương II

Bài tập: Ôn tập chương II (đề số 1)

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương