Tìm giá trị nguyên của n để giá trị biểu thức chia hết cho giá trị của biểu thức 3n + 1
 Giải bởi Vietjack
Giải bởi Vietjack
Ta có: =
Để phép chia đó là chia hết thì 4 ⋮ 3n + 1⇒ 3n + 1 ∈ Ư(4)
3n + 1 ∈ {-4; -2; -1; 1; 2; 4}
3n + 1 = -4⇒ 3n = -5⇒ n = 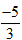
3n + 1 = -2⇒ 3n = -3⇒ n = -1 ∈ Z
3n + 1 = -1⇒ 3n = -2⇒ n = 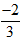
3n + 1 = 1⇒ 3n = 0⇒ n = 0 ∈ Z
3n + 1 = 2⇒ 3n = 2⇒ n = 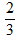
3n + 1 = 4⇒ 3n = 3⇒ n = 1 ∈ Z
Vậy n ∈ {-1; 0; 1} thì chia hết cho 3n + 1.
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Kết quả của phép tính là:
(A)
(B)
(C)
(D) .
Hãy chọn kết quả đúng.
Cho hai đa thức A = và B = . Tìm thương Q và số dư R sao cho A = B.Q + R.
Cho hai đa thức A=; B = .Tìm đa thức dư R trong phép chia A cho B rồi viết A= B.Q + R
Sắp xếp các đa thức sau theo lũy thừa giảm của biến rồi thực hiện phép chia:
Sắp xếp các đa thức sau theo lũy thừa giảm của biến rồi thực hiện phép chia:
Sắp xếp các đa thức sau theo lũy thừa giảm của biến rồi thực hiện phép chia: