Phương trình có nghiệm là:
A. x =
B. x = 2
C. x = 3
D. x = 5
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án D
Vậy phương trình có nghiệm là x = 5
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Một hình chữ nhật có chiều dài gấp 3 lần chiều rộng. Nếu cả chiều dài và chiều rộng cùng tăng thêm 5cm thì được một hình chữ nhật mới có diện tích bằng 153 cm2. Tìm chu vi hình chữ nhật ban đầu.
Cho hai số tự nhiên biết rằng hai lần số thứ nhất hơn ba lần số thứ hai là 9 và hiệu các bình phương của chúng bằng 119. Tìm số lớn hơn.
Cho tam giác vuông có cạnh huyền bằng 20 cm. Hai cạnh góc vuông có độ dài hơn kém nhau 4 cm. Một trong hai cạnh góc vuông của tam giác vuông có độ dài là:
Cho phương trình có biệt thức b = 2b'; . Phương trình đã cho có hai nghiệm phân biệt khi:
Gọi là nghiệm của phương trình . Không giải phương trình, tính giá trị của biểu thức
1. Hàm số y = ax2
a) Tập xác định
Cho hàm số
Tập xác định của hàm số là R.
b) Tính chất
+ Nếu a > 0 thì hàm số nghịch biến khi x < 0 và đồng biến khi x > 0.
+ Nếu a < 0 thì hàm số đồng biến khi x < 0 và nghịch biến khi x > 0.
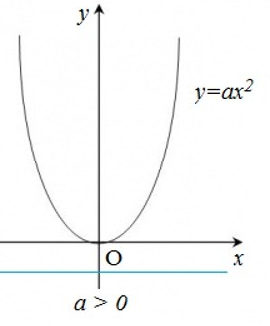
Đồ thị của hàm số là một đường cong đi qua gốc tọa độ và nhận trục Oy làm trục đối xứng. Đường cong đó được gọi là một parabol đỉnh O (với O là gốc tọa độ).
Tính chất của đồ thị:
+ Nếu a > 0 thì đồ thị nằm phía trên trục hoành, O là điểm thấp nhất của đồ thị.
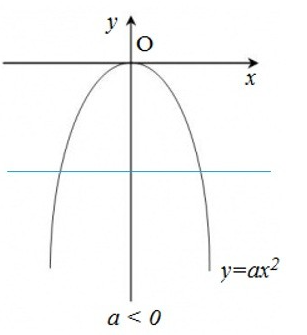
+ Nếu a < 0 thì đồ thị nằm phía dưới trục hoành, O là điểm cao nhất của đồ thị.
Bước 1: Tìm tập xác định của hàm số.
Bước 2: Lập bảng giá trị (thường từ 5 đến 7 giá trị) tương ứng giữa x và y.
Bước 3: Vẽ đồ thị và kết luận.
2. Phương trình bậc hai một ẩn
a) Định nghĩa: Phương trình bậc hai một ẩn (nói gọn là phương trình bậc hai) là phương trình có dạng
![]()
trong đó x là ẩn, a, b, c là những số cho trước gọi là các hệ số và .
b) Biệt thức
Đối với phương trình ax2 + bx + c = 0 (a ≠ 0) ta có biệt thức Δ như sau:
Δ = b2 - 4ac
Ta sửa dụng biết thức Δ để giải phương trình bậc hai.
c) Công thức nghiệm của phương trình bậc hai
Đối với phương trình ax2 + bx + c = 0 (a ≠ 0) và biệt thức Δ = b2 - 4ac
+ Nếu Δ > 0 thì phương trình có hai nghiệm phân biệt là
+ Nếu Δ = 0 thì phương trình có nghiệm kép là
+ Nếu Δ < 0 thì phương trình vô nghiệm.
d) Biệt thức
Đối với phương trình ax2 + bx + c = 0 (a ≠ 0) và b = 2b’ ta có biệt thức như sau:
= b’2 - ac
Ta sửa dụng biết thức để giải phương trình bậc hai.
e) Công thức nghiệm thu gọn của phương trình bậc hai
Đối với phương trình ax2 + bx + c = 0 (a ≠ 0) có b = 2b’ và biệt thức = b’2 - ac
+ Nếu > 0 thì phương trình có hai nghiệm phân biệt là
+ Nếu = 0 thì phương trình có nghiệm kép là
+ Nếu < 0 thì phương trình vô nghiệm.
3. Hệ thức Vi – ét
a) Hệ thức Vi – ét
Nếu x1, x2 là hai nghiệm của phương trình ax2 + bx + c = 0 (a ≠ 0) thì ta có:
b) Ứng dụng của hệ thức Vi - ét
+ Nếu phương trình ax2 + bx + c = 0 (a ≠ 0) có a + b + c = 0 thì phương trình có một nghiệm là x1 = 1 và nghiệm còn lại là
+ Nếu phương trình ax2 + bx + c = 0 (a ≠ 0) có a - b + c = 0 thì phương trình có một nghiệm là x1 = -1 và nghiệm còn lại là
+ Nếu hai số có tổng bằng S và tích bằng P thì hai số đó là nghiệm của phương trình bậc hai x2 - Sx + P = 0
+ Điều kiện để có hai số đó là S2 - 4P ≥ 0