Chiều cao của một tam giác vuông là 8cm chia cạnh huyền thành 2 đoạn thẳng hơn kém nhau 12cm. Tính độ dài cạnh huyền của tam giác vuông đó.
A. 14cm
B. 18cm
C. 16cm
D. 20cm
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án D
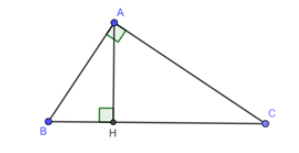
Giả sử tam giác vuông ABC có đường cao AH chia cạnh BC thành 2 đoạn thẳng BH và CH
Gọi độ dài cạnh BH là x (cm) (x > 0)
Khi đó độ dài cạnh CH là x + 12 (cm)
Áp dụng hệ thức lượng trong tam giác vuông ABC ta có:
Suy ra BH = 4cm và CH = 16cm
Vậy cạnh huyền BC = 20cm
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Một người dự định đi xe đạp từ A đến B cách nhau 36km trong thời gian đã định. Sau khi đi được nửa quãng đường, người đó dừng lại nghỉ 30 phút. Vì vậy mặc dù trên quãng đường còn lại đã tăng tốc thêm 2km/h song vẫn đến B chậm hơn dự kiến 12 phút. Vậy vận tốc của người đi xe đạp trên đoạn đường cuối của đoạn AB?
Tìm m để phương trình 3 + 4(m – 1)x + – 4m + 1 = 0 có hai nghiệm phân biệt thỏa mãn:
Cho phương trình 2 + 2mx + – 2 = 0, với m là tham số. Gọi là hai nghiệm của phương trình. Tìm hệ thức liên hệ giữa không phụ thuộc vào m.
Trong mặt phẳng tọa độ Oxy, cho đường thẳng (d): 2x – y – = 0 và parabol (P): y = a (a > 0). Tìm a để (d) cắt (P) tại hai điểm phân biệt A, B. Khi đó có kết luận gì về vị trí của hai điểm A, B
Cho parabol (P): y = và đường thẳng (d): y = mx + 1. Gọi A () và B () là các giao điểm của (d) và (P). Tìm m để biểu thức M = ( − 1)( − 1) đạt giá trị lớn nhất.
Tìm các giá trị của m để phương trình – mx + – m – 3 = 0 có hai nghiệm là độ dài các cạnh góc vuông của tam giác ABC tại A biết độ dài cạnh huyền BC = 2
Trong mặt phẳng tọa độ Oxy, cho parabol (P) có phương trình y = . Gọi (d) là đường thẳng đi qua I (0; −2) và có hệ số góc k. Đường thẳng (d) cắt parabol (P) tại hai điểm phân biệt A, B. Gọi H, K theo thứ tự là hình chiếu vuông góc của A, B trên trục hoành. Khi đó tam giác IHK là tam giác?
Phân tích đa thức f(x) = – 2m – x + – m thành tích của hai tam thức bậc hai ẩn x.
Tìm phương trình đường thẳng (d) đi qua điểm I (0; 1) và cắt parabol (P): y = tại hai điểm phân biệt M và N sao cho MN = 2
Một công nhân được giao làm một số sản phẩm trong thời gian nhất định. Khi còn làm nốt 30 sản phẩm cuối cùng người đó thấy nếu cứ giữ nguyên năng suất thì sẽ chậm 30 phút. Nếu tăng năng suất thêm 55 sản phẩm một giờ thì sẽ xong sớm hơn dự định là 30 phút. Tính năng suất của người thợ lúc đầu.
Một ô tô đi từ tỉnh A đến tỉnh B cách nhau 120km. Cùng lúc đó có một xe máy chạy từ B trở về A và gặp xe ô tô C cách một trong hai điểm khởi hành 75km. Tính vận tốc của mỗi xe, biết rằng nếu vận tốc của hai xe không đổi và xe máy khởi hành trước ô tô 48 phút thì sẽ gặp nhau ở giữa quãng đường.
Cho phương trình – 4x = 2|x – 2| − m – 5, với m là tham số. Xác định m để phương trình có bốn nghiệm phân biệt
Cho phương trình – (2m + 1)x + + 1 = 0, với m là tham số. Tìm tất cả các giá trị của m để phương trình có hai nghiệm phân biệt sao cho biểu thức có giá trị là số nguyên
Cho phương trình – (m – 1)x – + m – 2 = 0, với m là tham số. Gọi hai nghiệm của phương trình đã cho là . Tìm m để biểu thức đạt giá trị lớn nhất
Một phân xưởng đặt kế hoạch sản xuất 200 sản phẩm. Trong 5 ngày đầu do còn làm việc khác nên mỗi ngày phân xưởng sản xuất ít hơn mức đề ra là 4 sản phẩm. Trong những ngày còn lại, xưởng sản xuất vượt mức 10 sản phẩm mỗi ngày nên hoàn thành kế hoạch sớm hơn 1 ngày. Hỏi theo kế hoạch, mỗi ngày phân xưởng cần sản xuất bao nhiêu sản phẩm?
1. Hàm số y = ax2
a) Tập xác định
Cho hàm số
Tập xác định của hàm số là R.
b) Tính chất
+ Nếu a > 0 thì hàm số nghịch biến khi x < 0 và đồng biến khi x > 0.
+ Nếu a < 0 thì hàm số đồng biến khi x < 0 và nghịch biến khi x > 0.
Đồ thị của hàm số là một đường cong đi qua gốc tọa độ và nhận trục Oy làm trục đối xứng. Đường cong đó được gọi là một parabol đỉnh O (với O là gốc tọa độ).
Tính chất của đồ thị:
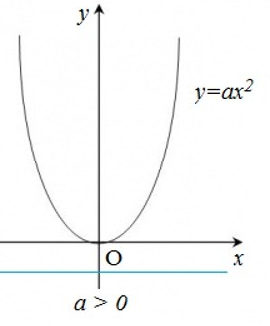
+ Nếu a > 0 thì đồ thị nằm phía trên trục hoành, O là điểm thấp nhất của đồ thị.
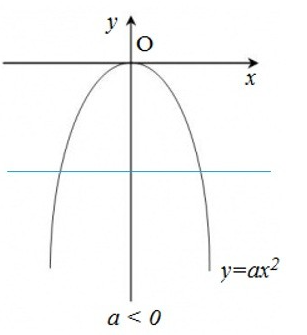
+ Nếu a < 0 thì đồ thị nằm phía dưới trục hoành, O là điểm cao nhất của đồ thị.
Bước 1: Tìm tập xác định của hàm số.
Bước 2: Lập bảng giá trị (thường từ 5 đến 7 giá trị) tương ứng giữa x và y.
Bước 3: Vẽ đồ thị và kết luận.
2. Phương trình bậc hai một ẩn
a) Định nghĩa: Phương trình bậc hai một ẩn (nói gọn là phương trình bậc hai) là phương trình có dạng
![]()
trong đó x là ẩn, a, b, c là những số cho trước gọi là các hệ số và .
b) Biệt thức
Đối với phương trình ax2 + bx + c = 0 (a ≠ 0) ta có biệt thức Δ như sau:
Δ = b2 - 4ac
Ta sửa dụng biết thức Δ để giải phương trình bậc hai.
c) Công thức nghiệm của phương trình bậc hai
Đối với phương trình ax2 + bx + c = 0 (a ≠ 0) và biệt thức Δ = b2 - 4ac
+ Nếu Δ > 0 thì phương trình có hai nghiệm phân biệt là
+ Nếu Δ = 0 thì phương trình có nghiệm kép là
+ Nếu Δ < 0 thì phương trình vô nghiệm.
d) Biệt thức
Đối với phương trình ax2 + bx + c = 0 (a ≠ 0) và b = 2b’ ta có biệt thức như sau:
= b’2 - ac
Ta sửa dụng biết thức để giải phương trình bậc hai.
e) Công thức nghiệm thu gọn của phương trình bậc hai
Đối với phương trình ax2 + bx + c = 0 (a ≠ 0) có b = 2b’ và biệt thức = b’2 - ac
+ Nếu > 0 thì phương trình có hai nghiệm phân biệt là
+ Nếu = 0 thì phương trình có nghiệm kép là
+ Nếu < 0 thì phương trình vô nghiệm.
3. Hệ thức Vi – ét
a) Hệ thức Vi – ét
Nếu x1, x2 là hai nghiệm của phương trình ax2 + bx + c = 0 (a ≠ 0) thì ta có:
b) Ứng dụng của hệ thức Vi - ét
+ Nếu phương trình ax2 + bx + c = 0 (a ≠ 0) có a + b + c = 0 thì phương trình có một nghiệm là x1 = 1 và nghiệm còn lại là
+ Nếu phương trình ax2 + bx + c = 0 (a ≠ 0) có a - b + c = 0 thì phương trình có một nghiệm là x1 = -1 và nghiệm còn lại là
+ Nếu hai số có tổng bằng S và tích bằng P thì hai số đó là nghiệm của phương trình bậc hai x2 - Sx + P = 0
+ Điều kiện để có hai số đó là S2 - 4P ≥ 0