Cho ABCD là hình thang vuông tại A và D. Đường chép BD vuông góc với BC. Biết AD = 10cm, DC = 20cm. Tính độ dài BC.
A. BC = 10 cm
B. BC = 10 cm
C. BC = 10cm
D. BC = cm
 Giải bởi Vietjack
Giải bởi Vietjack
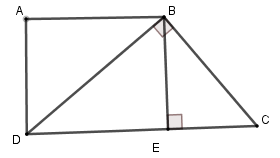
Kẻ BECD tại E
Suy ra tứ giác ABED là hình chữ nhật (vì ) nên BE = AD = 10cm
Đặt EC = x (0 < x < 20) thì DE = 20 – x
Áp dụng hệ thức giữa cạnh và đường cao trong tam giác vuông BCD ta có:
x(20 – x) = 100
x = 10 (tm)
Với EC = 10, theo định lý Pytago ta có BC =
Vậy BC =cm
Đáp án cần chọn là: B
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Cho tam giác ABC vuông tại A. Biết , đường cao AH = 42cm. Tính BH, HC
Tính diện tích hình thang ABCD có đường cao bằng 12cm, hai đường chéo AC và BD vuông góc với nhau, BD = 15cm.
Cho tam giác ABC vuông tại A, đường cao AH. Biết AB = 10cm, AH = 6cm. Tính độ dài các cạnh AC, BC của tam giác ABC.
“Trong tam giác vuông, bình phương đường cao ứng với cạnh huyền bằng…”. Cụm từ thích hợp điền vào chỗ trống là:
Cho ABC cân tại A, kẻ đường cao AH và CK. Biết AH = 7,5cm; CK = 12cm. Tính BC, AB
Cho ABC vuông tại A có AB = 3cm, AC = 4cm, đường cao AH và đường trung tuyến AM. Độ dài đoạn thẳng HM là:
Cho tam giác ABC vuông tại A, đường cao AH. Cho biết AB : AC = 3 : 4 và AH = 6cm. Tính độ dài các đoạn thẳng CH
Cho tam giác ABC vuông tại A, đường cao AH. Biết AB : AC = 5 : 12 và AB + AC = 34. Tính các cạnh của tam giác ABC
Cho tam giác ABC vuông tại A có cạnh AB = 30cm và AC = 40cm, đường cao AH, trung tuyến AM. Tính BH, HM, MC
Cho tam giác ABC vuông tại A có cạnh AB = 6cm và AC = 8cm. Các phân giác trong và ngoài của góc B cắt đường thẳng AC lần lượt tại M và N. Tính các đoạn thẳng AM và AN
Cho ABC vuông tại A, các cạnh AB, AC tương ứng tỉ lệ với 3 và 4. Biết đường cao AH = 18.
Tính chu vi ABC
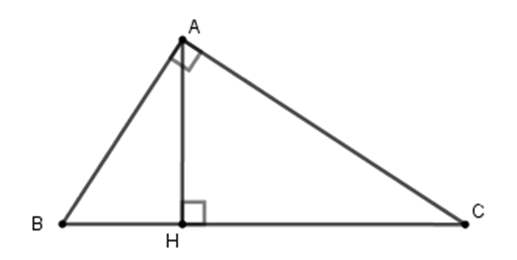
Cho tam giác ABC vuông tại A, đường cao AH (như hình vẽ). Hệ thức nào sau đây là sai?

Cho ABCD là hình tháng vuông A và D. Đường chéo BD vuông góc với BC. Biết AD = 12cm, DC = 25cm. Tính độ dài BC, biết BC < 20
1. Hệ thức giữa cạnh góc vuông và hình chiếu của nó trên cạnh huyền
Định lí 1. Trong một tam giác vuông, bình phương mỗi cạnh góc vuông bằng tích của cạnh huyền và hình chiếu của cạnh góc vuông đó trên cạnh huyền.
Ví dụ 1. Tam giác ABC vuông tại A, đường cao AH.
Khi đó, BH và CH lần lượt là hình chiếu của AB và AC trên BC.
Ta có: AB2 = BC . BH; AC2 = BC . HC.
2. Một số hệ thức liên quan tới đường cao
Định lí 2. Trong một tam giác vuông, bình phương đường cao ứng với cạnh huyền bằng tích hai hình chiếu của hai cạnh góc vuông trên cạnh huyền.
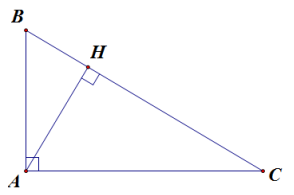
Ví dụ 2. Tam giác ABC vuông tại A, đường cao AH.
Khi đó, BH và CH lần lượt là hình chiếu của AB và AC trên BC.
Ta có: AH2 = BH . HC.
Định lí 3. Trong một tam giác vuông, tích hai cạnh góc vuông bằng tích của cạnh huyền và đường cao tương ứng.
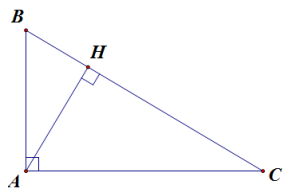
Ví dụ 3. Tam giác ABC vuông tại A, đường cao AH.
Khi đó, BH và CH lần lượt là hình chiếu của AB và AC trên BC.
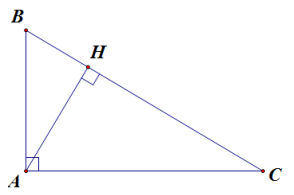
Ta có: AB . AC = BC . AH.
Định lí 4. Trong một tam giác vuông, nghịch đảo của bình phương đường cao ứng với cạnh huyền bằng tổng các nghịch đảo của bình phương hai cạnh góc vuông.
Ví dụ 4. Tam giác ABC vuông tại A, đường cao AH.
Khi đó, BH và CH lần lượt là hình chiếu của AB và AC trên BC.
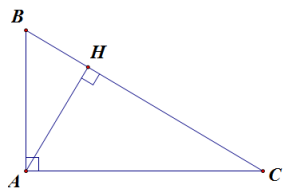
Ta có: .