Tính bán kính R của đường tròn đi qua cả bốn đỉnh của hình vuông ABCD cạnh 3cm
A.
B.
C. R = 3cm
D.
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án B
Gọi O là giao hai đường chéo của hình vuông ABCD. Khi đó theo tính chất của hình vuông ta có OA = OB = OC = OD nên O là tâm đường tròn ngoại tiếp hình vuông ABCD, bán kính
Xét tam giác ABC vuông cân tại B ta có
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Cho tam giác đều ABC cạnh bằng 2cm. Tính bán kính R của đường tròn ngoại tiếp tam giác ABC
Cho tam giác ABC vuông tại A, có AB = 5cm; AC = 12cm. Tính bán kính đường tròn ngoại tiếp tam giác ABC
Cho hình chữ nhật ABCD có AB = 8cm, BC = 6cm. Tính bán kính đường tròn đi qua bốn đỉnh A, B, C, D
Cho tam giác ABC có các đường cao BD, CE. Biết rằng bốn điểm B, E, D, C cùng nằm trên một đường tròn. Chỉ rõ tâm và bán kính của đường tròn đó.
Trên mặt phẳng tọa độ Oxy, xác định vị trí tương đối của điểm A (−3; −4) và đường tròn tâm là gốc tọa độ O, bán kính R = 3
Xác định tâm và bán kính của đường tròn đi qua cả bốn đỉnh của hình vuông ABCD cạnh a
Trên mặt phẳng tọa độ Oxy, xác định vị trí tương đối của điểm A (−1; −1) và đường tròn tâm là gốc tọa độ O, bán kính R = 2
Cho hình chữ nhật ABCD có AB = 12cm, BC = 5cm. Tính bán kính đường tròn đi qua bốn đỉnh A, B, C, D
Cho tam giác ABC vuông tại A, có AB = 15cm; AC = 20cm. Tính bán kính đường tròn ngoại tiếp tam giác ABC
1. Định nghĩa về đường tròn
Đường tròn tâm O bán kính R > 0 là hình gồm các điểm cách điểm O một khoảng R kí hiệu là (O; R) hay (O).
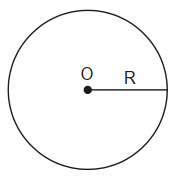
+ Điểm A nằm trên đường tròn (O; R) khi và chỉ khi OA = R.
+ Điểm A nằm trong đường tròn (O; R) khi và chỉ khi OA < R.
+ Điểm A nằm ngoài đường tròn (O; R) khi và chỉ khi OA > R.
Bổ sung kiến thức:
- Đường tròn đi qua các điểm A1, A2, ..., An gọi là đường tròn ngoại tiếp đa giác A1A2...An.
- Đường tròn tiếp xúc với tất cả các cạnh của đa giác A1A2...An gọi là đường tròn nội tiếp đa giác đó.
Ví dụ 1. Cho đường tròn (O; 5 cm). Biết độ dài OA = 5 cm, OB = 3 cm, OC = 8 cm. Xác định vị trí các điểm A, B, C đối với đường tròn (O).
Lời giải:
Ta có:
+ OA = 5 cm nên điểm A nằm trên đường tròn (O; 5 cm).
+ OB = 3 cm < 5 cm nên điểm B nằm trong đường tròn (O; 5 cm).
+ OC = 8 cm > 5 cm nên điểm C nằm ngoài đường tròn (O; 5 cm).
Ta có hình vẽ:
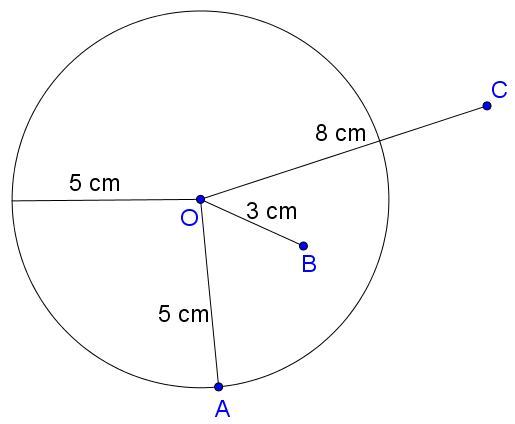
Vậy điểm A nằm trên đường tròn (O), điểm B nằm trong đường tròn (O) và điểm C nằm ngoài đường tròn (O).
2. Cách xác định đường tròn
Qua ba điểm không thẳng hàng, ta vẽ được một và chỉ một đường tròn.
Chú ý: Không vẽ được đường tròn nào đi qua 3 điểm thẳng hàng.
• Trong tam giác vuông: tâm đường tròn ngoại tiếp là trung điểm của cạnh huyền.
• Trong tam giác đều: tâm đường tròn ngoại tiếp là trọng tâm tam giác đó.
• Trong tam giác thường:
+ Tâm đường tròn ngoại tiếp là giao điểm của ba đường trung trực của ba cạnh tam giác đó.
+ Tâm đường tròn nội tiếp là giao điểm ba đường phân giác trong của tam giác đó.
Ví dụ 1.
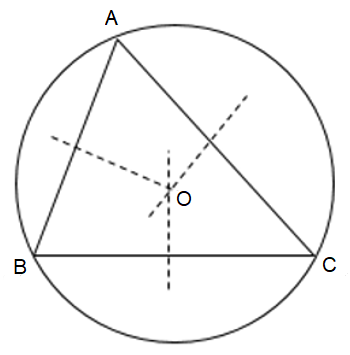
+ Ba đường trung trực của ba cạnh của ∆ABC cắt nhau tại điểm O.
Khi đó, O là tâm đường tròn ngoại tiếp ∆ABC.
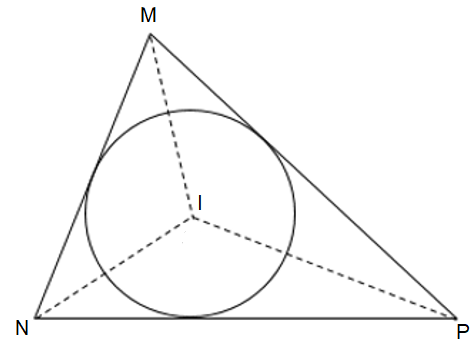
+ Ba đường phân giác của ba cạnh của ∆MNP cắt nhau tại điểm I.
Khi đó, I là tâm đường tròn nội tiếp ∆MNP.
3. Tâm đối xứng
Đường tròn là hình có tâm đối xứng. Tâm của đường tròn là tâm đối xứng của đường tròn đó.
Ví dụ 2. Cho đường tròn (O), A là một điểm bất kì thuộc đường tròn. Vẽ A’ đối xứng với A qua O. Chứng minh rằng điểm A’ cũng thuộc đường tròn (O).
Lời giải:
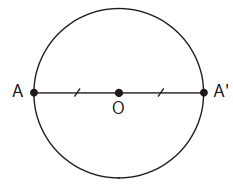
Do A' đối xứng với A qua O nên O là trung điểm của AA'.
Khi đó, OA = OA' = R.
Do đó, điểm A' nằm trên đường tròn (O).
Vậy điểm A' cũng thuộc đường tròn (O).
4. Trục đối xứng
Đường tròn là hình có trục đối xứng. Bất kỳ đường kính nào của đường tròn cũng là trục đối xứng của đường tròn.
Ví dụ 3. Cho đường tròn (O), AB là một đường kính bất kì và M là một điểm thuộc đường tròn (O). Lấy điểm N đối xứng với điểm N qua AB.
Khi đó, điểm N cũng thuộc đường tròn (O).