Trên mặt phẳng tọa độ Oxy, cho điểm A (−2; 3). Hãy xác định vị trí tương đối của đường tròn (A; 2) và các trục tọa độ
A. Trục tung cắt đường tròn và trục hoành tiếp xúc với đường tròn
B. Trục hoành không cắt đường tròn và trục tung tiếp xúc với đường tròn
C. Cả hai trục tọa độ đều cắt đường tròn
D. Cả hai trục tọa độ đều tiếp xúc với đường tròn
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án B
Vì A (−2; 3) nên khoảng cách từ A đến trục hoành là , khoảng cách từ A đến trục tung là
Nhận thấy nên trục tung tiếp xúc với đường tròn (A; 2)
Và nên trục hoành không cắt đường tròn (A; 2)
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Trên mặt phẳng tọa độ Oxy, cho điểm A (4; 5). Hãy xác định vị trí tương đối của đường tròn (A; 5) và các trục tọa độ
Đường thẳng a cách tâm O của đường tròn (O; R) một khoảng bằng cm. Biết R = 3cm; số giao điểm của đường thẳng a và đường tròn (O; R) là:
Cho . Đường tròn (I) là đường tròn tiếp xúc với cả hai cạnh Ox; Oy. Khi đó điểm I chạy trên đường nào?
Cho đường tròn tâm O bán kính 3cm và một điểm A cách O là 5cm. Kẻ tiếp tuyến AB với đường tròn (B là tiếp điểm). Tính độ dài AB
Cho a, b là hai đường thẳng song song và cách nhau một khoảng 2,5cm. Lấy điểm I trên a và vẽ đường tròn (I; 2,5cm). Khi đó đường tròn với đường thẳng b
Cho a, b là hai đường thẳng song song và cách nhau một khoảng 3cm. Lấy điểm I trên a và vẽ đường tròn (I; 3,5cm). Khi đó đường tròn với đường thẳng b
Cho đường tròn tâm O bán kính 6cm và một điểm A cách O là 10cm. Kẻ tiếp tuyến AB với đường tròn (B là tiếp điểm). Tính độ dài AB
1. Ba vị trí tương đối của đường thẳng và đường tròn
a) Đường thẳng và đường tròn cắt nhau
Khi đường thẳng a và đường tròn (O) có hai điểm chung A và B, ta nói đường thẳng a và đường tròn (O) cắt nhau. Đường thẳng a còn gọi là cát tuyến của đường tròn (O).
Gọi OH là khoảng cách từ điểm O đến đường thẳng a.
+ Trường hợp 1: Đường thẳng a đi qua điểm O.
Khi đó, AB là đường kính và O ≡ H (hay OH = 0).
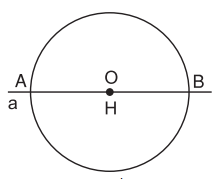
Do đó: HA = HB = R = (1)
+ Trường hợp 2: Đường thẳng a không đi qua điểm O.
Khi đó, AB là dây của đường tròn (O) và .
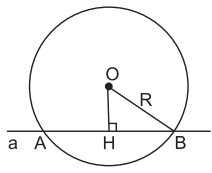
Xét ∆OBH vuông tại H, theo định lý Py-ta-go:
(2)
Từ (1) và (2) suy ra .
b) Đường thẳng và đường tròn tiếp xúc nhau
Khi đường thẳng a và đường tròn (O) chỉ có một điểm chung C, ta nói đường thẳng a và đường tròn (O) tiếp xúc nhau. Ta nói đường thẳng a là tiếp tuyến của đường tròn (O). Điểm C gọi là tiếp điểm.
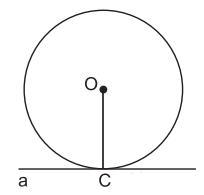
Định lí. Nếu một đường thẳng là tiếp tuyến của một đường tròn thì nó vuông góc với bán kính đi qua tiếp điểm.
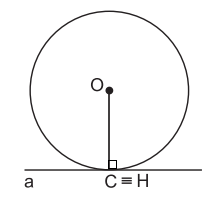
Ví dụ 1. Đường thẳng a là tiếp tuyến của đường tròn (O), C là tiếp điểm của đường tròn (O) thì OC là bán kính.
Khi đó, đường thẳng a vuông góc với bán kính đi qua tiếp điểm C.
Gọi OH là khoảng cách từ điểm O đến đường thẳng a.
Do đó H trùng với C, và OH = R.
c) Đường thẳng và đường tròn không giao nhau
Khi đường thẳng a và đường tròn (O) không có điểm chung, ta nói đường thẳng a và đường tròn (O) không giao nhau.
Gọi OH là khoảng cách từ điểm O đến đường thẳng a.
Khi đó, OH > R.
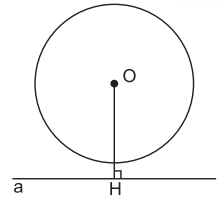
2. Hệ thức giữa khoảng cách từ tâm đường tròn đến đường thẳng và bán kính của đường tròn
|
Vị trí tương đối của đường thẳng và đường tròn |
Số điểm chung |
Hệ thức giữa d và R |
|
Đường thẳng và đường tròn cắt nhau |
2 |
d < R |
|
Đường thẳng và đường tròn tiếp xúc nhau |
1 |
d = R |
|
Đường thẳng và đường tròn không giao nhau |
0 |
d > R |
Ví dụ 2. Cho đường tròn (O; 6), đường thẳng a cách điểm O là 4. Đường thẳng a có vị trí như thế nào đối với đường tròn (O) ?
Lời giải:
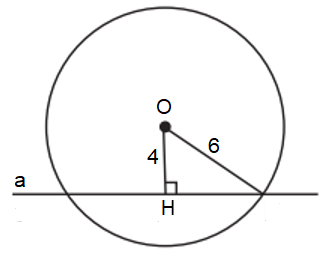
Gọi OH là khoảng cách từ điểm O đến đường thẳng a.
Ta có OH < R (vì 4 < 6).
Do đó, đường thẳng a cắt đường tròn (O) tại 2 điểm phân biệt.