Cho tam giác ABC vuông ở A. vẽ hai nửa đường tròn đường kính AB và AC ra phía ngoài của tam giác. Qua A vẽ cát tuyến MAN (M thuộc nửa đường tròn đường kính AB, N thuộc nửa đường tròn đường kính AC)
a) Tứ giác BCNM là hình gì?
b) Tìm quỹ tích trung điểm I của đoạn MN khi cát tuyến MAN quay quanh A.
 Giải bởi Vietjack
Giải bởi Vietjack
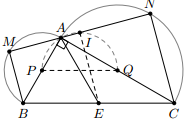
a) Vì M, N lần lượt nằm trên nửa đường tròn đường kính AB, AC nên
Do đó => BMCN là hình thang vuông (tại M, N)
b) Tìm quỹ tích trung điểm I của đoạn MN:
- Phần thuận:
Gọi E là trung điểm BC => IE là đường trung bình của hình thang BCNM
, do đó
Vậy điểm M nằm trên đường tròn đường kính AE.
- Giới hạn:
Gọi P, Q lần lượt là trung điểm của AB, AC. Ta có APEQ là hình chữ nhật nên P, Q cùng nằm trên đường tròn đường kính AE.
+ Nếu
+ Nếu
Vậy điểm M chỉ nằm trên cung của đường tròn đường kính AE.
- Phần đảo:
Lấy điểm I trên cung của đường tròn đường kính AE. Nối AI lần lượt cắt tại M, N.
Ta có (góc nội tiếp chắn nửa đường tròn) nên => EI // BM
Do đó EI là đường trung bình của hình thang BCNM => MI = NI
- Kết luận: quỹ tích điểm I nằm trên cung của đường tròn đường kính AE.
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Cho hình vuông ABCD. Trên cạnh BC lấy điểm E, trên tia đối của tia CD lấy điểm F sao cho CE = CF. Gọi M là giao điểm của hai đường thẳng DE và BF. Tìm quỹ tích điểm M khi E di động trên cạnh BC.
Cho hình thang cân ABCD (AB // CD). Chứng minh rằng bốn điiểm A, B, C, D cùng thuộc một đường tròn.
Xét tam giác ABC có BC = 2 cm cố định và
a) Tìm quỹ tích các điểm A
b) Điểm A ở vị trí nào thì diện tích có diện tích lớn nhất? Tính giá trị lớn nhất đó.
Cho vuông ở A, có cạnh BC cố định. Gọi I là giao điểm của ba đường phân giác trong. Tìm quỹ tích I khi A thay đổi.
Dựng tam giác ABC biết:
a) BC = 8cm, và đường cao AH = 6cm.
b) BC = 8cm, và đường cao AH = cm.
c) BC = 4cm, và đường cao AH = 9 cm.
Cho nửa đường tròn đường kính AB và cung EF của nửa đường tròn (E nằm trên cung AF sao cho sd ). Hai tia AE và BF cắt nhau tại M. Tìm quỹ tích các điểm M khi cung chuyển động trên nửa đường tròn.
Cho nửa đường tròn đường kính AB cố định và điểm C di chuyển trên nửa đường tròn. Ở phía ngoài tam giác ABC, vẽ tam giác BCD vuông cân tại C. Tìm quỹ tích điểm D.
Dựng tam giác ABC biết
a) BC = 6cm, và trung tuyến AM = 5cm.
b) BC = 4cm, và trung tuyến AM = cm.
Cho cung một phần tư đường tròn với hai bán kính OA, OB vuông góc với nhau. Trên cung này lấy một điểm C tùy ý không trùng với A và B. Vẽ CH vuông góc với OA. Gọi I là tâm đường tròn nội tiếp tam giác HOC.
a) Chứng minh rằng
b) Tìm quỹ tích điểm I khi điểm C di động trên cung AB.
Cho hai điểm A, B cố định. Từ A vẽ các tiếp tuyến với đường tròn tâm B có bán kính không lớn hơn AB. Tìm quỹ tích các tiếp điểm.
Cho tam giác ABC có , nội tiếp đường tròn (O). Trên cung nhỏ AC lấy một điểm D, trên dây BD lấy điểm M sao cho DM = CD.
a) Chứng minh tam giác MCD là tam giác đều.
b) Tìm quỹ tích điểm M khi điểm D di động trên cung nhỏ AC.
Xét có BC = 6 cm, cố định,
a) Tìm quỹ tích các điểm A
b) Điểm A ở vị trí nào thì có diện tích lớn nhất? Tính giá trị lớn nhất đó?