Bài tập Cung chứa góc có đáp án
-
2243 lượt thi
-
23 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
Cho vuông ở A, có cạnh BC cố định. Gọi I là giao điểm của ba đường phân giác trong. Tìm quỹ tích I khi A thay đổi.
 Xem đáp án
Xem đáp án
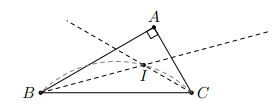
Phần thuận: Ta có:
Vì B, C cố định, A thay đổi, I luôn nhìn cạnh BC dưới một góc nên I di chuyển trên cung chứa góc dựng trên BC.
Phần đảo: Lấy điểm I là giao của cung chứa góc dựng trên BC và tia phân giác trong góc , ta chứng minh I cũng thuộc tia phân giác trong của góc .
Xét tam giác IBC, ta có:
Nên BI là phân giác trong của . Hay I là tâm đường tròn nội tiếp (I là giao điểm của ba đường phân giác trong)
Giới hạn:
- Khi thì ba điểm A, B, C thẳng hàng (trái giả thiết)
- Khi thì ba điểm A, B, C thẳng hàng (trái giả thiết)
Vậy quỹ tích điểm I là cung chứa góc dựng trên cạnh BC đối xứng nhau qua BC, bỏ đi điểm B và C.
Kết luận: Quỹ tích điểm I là cung chứa góc dựng trên cạnh BC đối xứng nhau qua BC, bỏ đi điểm B và C.
Câu 2:
Cho hai điểm A, B cố định. Từ A vẽ các tiếp tuyến với đường tròn tâm B có bán kính không lớn hơn AB. Tìm quỹ tích các tiếp điểm.
 Xem đáp án
Xem đáp án
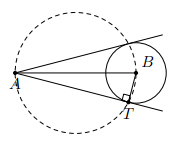
Phần thuận: Theo tính chất của tiếp tuyến ta có:
Do đó, A, B cố định. T nhìn AB dưới một góc vuông nên T di chuyển trên đường trong đường kính AB.
Phần đảo: lấy điểm T thuộc đường tròn đường kính AB.
Khi đó tại T nên AT là tiếp tuyến của đường tròn tâm B, bán kính
Giới hạn:
- Khi thì bán kính đường tròn tâm B thỏa yêu cầu đề bài là 0 (vô lí)
- Khi thì bán kính đường tròn tâm B thỏa yêu cầu đề bài là AB.
Vậy quỹ tích tiếp điểm T là đường tròn đường kính AB bỏ đi điểm B.
Kết luận: Quỹ tích tiếp điểm T là đường tròn đường kính AB bỏ đi điểm B.
Câu 3:
Xét có BC = 6 cm, cố định,
a) Tìm quỹ tích các điểm A
b) Điểm A ở vị trí nào thì có diện tích lớn nhất? Tính giá trị lớn nhất đó?
 Xem đáp án
Xem đáp án
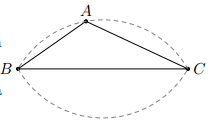
a) Ta thực hiện theo các phần:
Phần thuận: Do BC cố định, nên A di chuyển trên hai cung chứa góc dựng trên BC.
Phần đảo: lấy điểm A thuộc cung chứa góc dựng trên BC, ta thấy ngay
Giới hạn: Khi A trùng với B, C thì ba điểm A, B, C thẳng hàng (trái giả thiết)
Vậy quỹ tích các điểm A là hai cung chứa góc dựng trên đoạn BC, bỏ đi điểm B, C.
Kết luận: Quỹ tích các điểm A là hai cung chứa góc dựng trên đoạn BC, bỏ đi điểm B, C.
b) Hạ AH vuông góc với BC, ta có ngay:
Do đó, có giá trị nhỏ nhất khi AH lớn nhất <=> A là điểm ở chính giữa cung chứa góc.
Khi đó, xét vuông tại H, ta có
Xét tam giác ABH ta có
Câu 4:
Cho nửa đường tròn đường kính AB và cung EF của nửa đường tròn (E nằm trên cung AF sao cho sd ). Hai tia AE và BF cắt nhau tại M. Tìm quỹ tích các điểm M khi cung chuyển động trên nửa đường tròn.
 Xem đáp án
Xem đáp án
Phần thuận: giả sử có điểm M sao cho , ta có:
Vậy điểm M nằm trên cung chứa góc dựng trên đoạn thẳng AB (cung này thuộc mặt phẳng bờ AB có chứa nửa đường tròn cho trước)
Giới hạn: ta có:
- Nếu => , với là giao điểm của cung chứa góc với tiếp tuyến Ax của nửa đường tròn đường kính AB.
- Nếu => , với là giao điểm của cung chứa góc với tiếp tuyến By của nửa đường tròn dường kính Ab. Do đó, điểm M chỉ nằm trên cung
Phần đảo: lấy điểm M nằm trên cung . Nối MA, MB cắt nửa đường tròn đường kính AB lần lượt tại E và F. Ta phải chứng minh số đo
Thật vậy:
Kết luận: quỹ tích các điểm M là cung của cung chứa góc dựng trên đoạn thẳng AB (cung này thuộc nửa mặt phẳng bờ AB có chứa nửa đường tròn đã cho)
Câu 5:
Dựng cung chứa góc trên đoạn AB = 4 cm.
 Xem đáp án
Xem đáp án
Ta lần lượt thực hiện:
- Dựng đoạn AB = 4 cm và đường trung trực của AB
- Dựng tia Ax sao cho
- Dựng tia Ay vuông góc với Ax cắt tại O.

- Dựng đường tròn (O;OA) và chỉ lấy phần cung cùng phía với O, kí hiệu là
- Lấy đối xứng cung qua Ab được cung .
Vậy hai cung và là cung chứa góc cần dựng.
Câu 6:
Dựng , biết BC = 6 cm, và đường cao AH = 4 cm.
 Xem đáp án
Xem đáp án
Cách dựng:
- Dựng đoạn thẳng BC = 6 cm.
- Dựng cung chứa góc trên đoạn thẳng BC.
- Dựng đường thẳng d song song với BC và cách BC một khoảng bằng 4 cm, như sau: Dựng đường trung trực của BC, gọi I là giao điểm của với BC, trên lấy điểm K sao cho IK = 4 cm.
- Dựng đường thẳng d vuông góc với tại K.
- Gọi giao điểm của (d) và cung chứa góc là A và A’. khi đó, hai tam giác ABC và A’BC đều thỏa mãn yêu cầu bài toán.
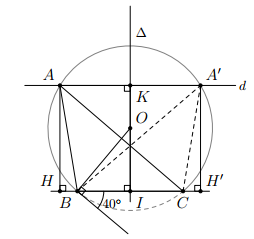
Chứng minh:
- Ta có ngay BC = 6 cm vì theo cách dựng.
- Các góc và đều bằng do A, A’ nằm trên cung chứa góc dựng trên đoạn BC.
- Các hình AHIK và A’HIK là các hình chữ nhật nên AH = A’H = IK = 4 cm.
Biện luận: ta dựng được hai tam giác ABC và A’BC thỏa điều kiện đề bài nhưng hai tam giác này bằng nhau (đối xứng nhau qua IK) nên bài toán chỉ có một nghiệm hình.
Câu 7:
Dựng biết BC = a, và đường cao BH = h với h < a
 Xem đáp án
Xem đáp án
Cách dựng: ta lần lượt thực hiện:
- Dựng đoạn BC = a.
- Dựng cung chứa góc dựng trên đoạn thẳng BC.
- Dựng đường tròn đường kính BC.
- Dựng đường tròn (B, h) cắt đường tròn đường kính BC tại H.
- Tia CH cắt cung chứa góc tại A.
- Nối AB ta được phải dựng
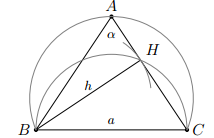
Chứng minh: ta có ngay:
- BC = a theo cách dựng.
- vì A nằm trên cung chứa góc dựng trên đoạn thẳng BC.
- BH = h vì H thuộc đường tròn (B, h)
- => Bh = h là đường cao của
Vậy thỏa mãn điều kiện đầu bài.
Biện luận: ta dựng dược hai tam giác ABC và A’BC thỏa mãn điều kiện đề bài, nhưng hai tam giác này bằng nhau (đối xứng qua BC) nên bài toán chỉ có một nghiệm hình.
Câu 8:
Cho I, O lần lượt là tâm đường tròn nội tiếp, tâm đường tròn ngoại tiếp của tam giác ABC với , gọi H là giao điểm của các đường cao BB’ và CC’. Chứng minh các điểm A, B, O, H, I cùng thuộc một đường tròn.
 Xem đáp án
Xem đáp án
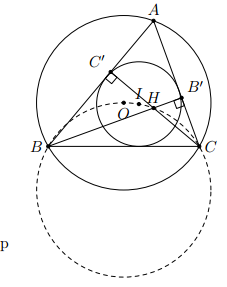
Xét tứ giác AB’HC’ ta có:
Xét ta có:
Như vậy, H và I đều nằm trên cung chứa góc dựng trên BC.
Mặt khác, nội tiếp trong đường tròn tâm O nên góc nội tiếp trong đường tròn (O) có số đo là
Vậy O nằm trên cung chứa góc dựng trên BC.
Nghĩa là 5 điểm B, C, O, I, H nằm trên cùng một đường tròn chứa cung chứa góc dựng trên BC.
Câu 9:
Cho hình thang cân ABCD (AB // CD). Chứng minh rằng bốn điiểm A, B, C, D cùng thuộc một đường tròn.
 Xem đáp án
Xem đáp án
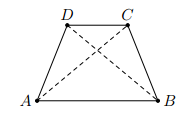
Xét hai tam giác và , ta có:
CD chung
, vì ABCD là hình thang cân.
AD = BC, vì ABCD là hình thang cân.
Do đó:
=>
Vậy các điểm A, B nằm cùng phía đối với CD và thỏa mãn nên bốn điểm A, B, C, D cùng thuộc một đường tròn.
Câu 10:
Cho cân tại A. Lấy hai điểm E, F theo thứ tự thuộc AB, AC sao cho AE = AF. Chứng minh rằng bốn điểm B, C, E, F cùng thuộc một đường tròn.
 Xem đáp án
Xem đáp án
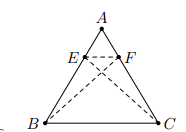
Xét hai tam giác ta có:
AB = AC, vì cân tại A
chung
AE = AF, giả thiết
Do đó:
Vậy các điểm B, C nằm phía dưới đối với EF và thỏa mãn nên bốn điểm B, C, E, F cùng thuộc một đường tròn.
Câu 11:
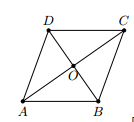
Cho các hình thoi ABCD có cạnh AB cố định. Tìm quỹ tích giao điểm O của hai đường chéo của hình thoi đó.
 Xem đáp án
Xem đáp án
Vì ABCD là hình thoi nên . Do AB cố định nên O chạy trên đường tròn đường kính AB.
Câu 12:
Xét tam giác ABC có BC = 2 cm cố định và
a) Tìm quỹ tích các điểm A
b) Điểm A ở vị trí nào thì diện tích có diện tích lớn nhất? Tính giá trị lớn nhất đó.
 Xem đáp án
Xem đáp án
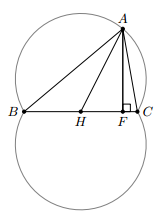
a) Vì BC = 2 cm và nên quỹ tích các điểm A là cung chứa góc nhìn BC dưới một góc
b) Gọi AF là đường cao hạ từ A xuống BC và H là trung điểm BC. Khi đó:
Vậy diện tích lớn nhất khi A là điểm chính giữa cung . Khi đó là tam giác đều có cạnh bằng 2 cm, do đó diện tích tam giác ABC lớn nhất bằng
Câu 13:
Cho nửa đường tròn đường kính AB và cung EF của nửa đường tròn (E nằm trên cung sao cho sđ . Hai tia AE và BF cắt nhau tại M. Tìm quỹ tích điểm M khi cung chuyển động trên nửa đường tròn.
 Xem đáp án
Xem đáp án
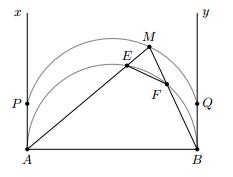
- Phần thuận:
Giả sử có điểm M sao cho sđ , khi đó
Vậy điểm M nằm trên cung chứa góc dựng trên đoạn AB (cung này thuộc nửa mặt phẳng bờ AB có chứa nửa đường tròn cho trước)
- Giới hạn:
Gọi P, Q lần lượt là giao điểm của tiếp tuyến Ax, By (của nửa đườn tròn đường kính AB với cung chứa góc chứa điểm M)
+ nếu
+ nếu
Vậy điểm M chỉ nằm trên cung
- Phần đảo:
Lấy điểm M trên cung . Nối MA, MB cắt nửa đường tròn đường kính AB lần lượt tại E và F.
Ta có:
Kết luận: quỹ tích điểm M chỉ nằm trên cung (cung này thuộc nửa mặt phẳng bờ AB có chứa nửa đường tròn cho trước)
Câu 14:
Cho hình vuông ABCD. Trên cạnh BC lấy điểm E, trên tia đối của tia CD lấy điểm F sao cho CE = CF. Gọi M là giao điểm của hai đường thẳng DE và BF. Tìm quỹ tích điểm M khi E di động trên cạnh BC.
 Xem đáp án
Xem đáp án

- Phần thuận:
Xét hai tam giác vuông có
BC = CD (do ABCD là hình vuông)
CE = CF (gt) nên
Do đó,
Mà (đối đỉnh) nên
Vậy điểm M nằm trên đường tròn đường kính BD.
- Giới hạn:
+ Nếu
+ Nếu
Vậy điểm M chỉ nằm trên cung nhỏ của đường tròn đường kính BD.
- Phần đảo:
Lấy điểm M trên cung nhỏ của đường tròn đường kính BD. Nối MB, MD lần lượt cắt CD, BC tại F, E
Ta có (góc nội tiếp chắn nửa đường tròn) nên do đó CF = CE.
- Kết luận: quỹ tích điểm M nằm trên cung nhỏ của đường tròn đường kính BD.
Câu 15:
Cho tam giác ABC vuông ở A. vẽ hai nửa đường tròn đường kính AB và AC ra phía ngoài của tam giác. Qua A vẽ cát tuyến MAN (M thuộc nửa đường tròn đường kính AB, N thuộc nửa đường tròn đường kính AC)
a) Tứ giác BCNM là hình gì?
b) Tìm quỹ tích trung điểm I của đoạn MN khi cát tuyến MAN quay quanh A.
 Xem đáp án
Xem đáp án
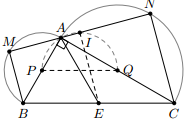
a) Vì M, N lần lượt nằm trên nửa đường tròn đường kính AB, AC nên
Do đó => BMCN là hình thang vuông (tại M, N)
b) Tìm quỹ tích trung điểm I của đoạn MN:
- Phần thuận:
Gọi E là trung điểm BC => IE là đường trung bình của hình thang BCNM
, do đó
Vậy điểm M nằm trên đường tròn đường kính AE.
- Giới hạn:
Gọi P, Q lần lượt là trung điểm của AB, AC. Ta có APEQ là hình chữ nhật nên P, Q cùng nằm trên đường tròn đường kính AE.
+ Nếu
+ Nếu
Vậy điểm M chỉ nằm trên cung của đường tròn đường kính AE.
- Phần đảo:
Lấy điểm I trên cung của đường tròn đường kính AE. Nối AI lần lượt cắt tại M, N.
Ta có (góc nội tiếp chắn nửa đường tròn) nên => EI // BM
Do đó EI là đường trung bình của hình thang BCNM => MI = NI
- Kết luận: quỹ tích điểm I nằm trên cung của đường tròn đường kính AE.
Câu 16:
Cho nửa đường tròn đường kính AB cố định và điểm C di chuyển trên nửa đường tròn. Ở phía ngoài tam giác ABC, vẽ tam giác BCD vuông cân tại C. Tìm quỹ tích điểm D.
 Xem đáp án
Xem đáp án
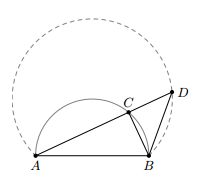
- Phần thuận:
Ta có nên A, C, D thẳng hàng.
Vì tam giác BCD vuông cân tại C nên , do đó điểm D nằm trên cung chứa góc dựng trên đoạn AB (cung thuộc nửa mặt phẳng bờ AB có chứa nửa đường tròn cho trước)
- Giới hạn:
+ nếu
+ nếu
Vậy điểm D nằm trên cung chứa góc dựng trên đoạn AB.
- Phần đảo:
Lấy điểm D trên cung chứa góc dựng trên đoạn AB. Nối AD với nửa đường tròn AB tại C
Ta có (góc nội tiếp chắn nửa đường tròn) và nên vuông cân tại C, do đó CB = CD.
- Kết luận: quỹ tích điểm D nằm trên cung chứa góc dựng trên dây AB.
Câu 17:
Cho tam giác ABC có , nội tiếp đường tròn (O). Trên cung nhỏ AC lấy một điểm D, trên dây BD lấy điểm M sao cho DM = CD.
a) Chứng minh tam giác MCD là tam giác đều.
b) Tìm quỹ tích điểm M khi điểm D di động trên cung nhỏ AC.
 Xem đáp án
Xem đáp án
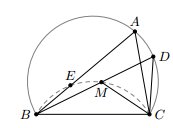
Vì nên
Do đó tam giác MDC đều (vì DM = DC)
b) Tìm quỹ tích điểm M:
- Phần thuận:
Vì tam giác MDC đều nên , do đó điểm M chạy trên cung chứa góc dựng trên đoạn BC.
- Giới hạn:
Gọi E là giao điểm của AB và cung chứa góc dựng trên đoạn BC.
+ nếu
+ nếu
Vậy điểm M chỉ nằm trên cung nhỏ của cung chứa góc dựng trên đoạn BC.
- Phần đảo:
Lấy điểm M trên cung nhỏ của cung chứa góc dựng trên đoạn BC. Nối BM cắt (O) tại D.
Ta có (góc nội tiếp) nên
Mà nên tam giác MCD đều, do đó DC = DM.
Kết luận: quỹ tích điểm M nằm trên cung nhỏ của cung chứa góc dựng trên đoạn BC.
Câu 18:
Cho cung một phần tư đường tròn với hai bán kính OA, OB vuông góc với nhau. Trên cung này lấy một điểm C tùy ý không trùng với A và B. Vẽ CH vuông góc với OA. Gọi I là tâm đường tròn nội tiếp tam giác HOC.
a) Chứng minh rằng
b) Tìm quỹ tích điểm I khi điểm C di động trên cung AB.
 Xem đáp án
Xem đáp án
a) Xét hai tam giác AIO và CIO có:
OA = OC
OI chung
Nên
b) Tìm quỹ tích điểm I khi C di động trên cung AB.
- Phần thuận:
Ta có:
Vì A, O cố định nên quỹ tích điểm I nằm trên cung dựng trên đoạn AO.
- Giới hạn:
Vì C chỉ chạy trên cung nên điểm I chỉ chạy trên cung chứa góc dựng trên đoạn AO thuộc nửa mặt phẳng bờ AO có chứa điểm B.
- Phần đảo:
Lấy điểm I trên cung chứa góc dựng trên đoạn AO. Dựng OC sao cho OI là tia phân giác góc (C nằm trên cung), từ C hạ
Vì nên , do vậy C, I, H, A cùng nằm trên cùng một đường tròn.
Từ đó suy ra => IC là tia phân giác góc , vì vậy I là tâm đường tròn nội tiếp tam giác COH.
- Kết luận: quỹ tích điểm I là cung chứa góc dựng trên đoạn AO thuộc nửa mặt phẳng bờ AO có chứa điểm B.
Câu 19:
Dựng tam giác ABC biết BC = 3cm, , AB = 2cm.
 Xem đáp án
Xem đáp án

a) Cách dựng:
- Dựng đoạn BC = 3 cm
- Dựng cung chứa góc trên đoạn BC
- Dựng đường tròn (B; 2cm) cắt cung chứa góc ở trên tại A.
- Nối AB, AC ta được tam giác ABC.
b) Chứng minh:
- Ta có BC = 3 cm (cách dựng)
-
- AB = 2 cm (do A nằm trên (B; 2 cm)
c) Biện luận:;
Ta dựng được hai tam giác ABC và A’BC (đối xứng qua BC) thỏa mãn yêu cầu đề bài.
Do hai tam giác này bằng nhau nên ta chỉ có mọt nghiệm hình (do đây là bài toán dựng hình về kích thước).
Câu 20:
Dựng tam giác ABC biết:
a) BC = 4cm, và đường cao BH = 3 cm.
b) BC = 6cm, và đường cao BH = 4 cm.
 Xem đáp án
Xem đáp án
a)

* Cách dựng
- Dựng đoạn BC = 4 cm.
- Dựng cung chứa góc trên đoạn BC.
- Dựng đường tròn đường kính BC.
- Dựng đường tròn (B;3cm) cắt đường tròn đường kính BC tại H.
- Tia Ch cắt cung chứa góc (ở trên) tại A.
- Nối AB ta được tam giác ABC cần dựng.
* Chứng minh:
Ta có:
- BC = 4 cm (cách dựng)
- vì nằm trên cung chứa góc trên đoạn BC.
- BH = 3 cm vì H nằm trên đường tròn (B; 3 cm)
- là góc nội tiếp chắn nửa đường tròn.
Vậy tam giác ABC thỏa mãn yêu cầu bài toán.
* Biện luận:
Ta dựng được hai tam giác ABC và A’BC (đối xứng nhau qua BC) thỏa mãn yêu cầu đề bài.
Do hai tam giác này bằng nhau nên ta chỉ có một nghiệm hình (do đây là bài toán dựng hình về kích thước)
b) Tương tự câu a).
Câu 21:
Dựng tam giác ABC biết:
a) BC = 8cm, và đường cao AH = 6cm.
b) BC = 8cm, và đường cao AH = cm.
c) BC = 4cm, và đường cao AH = 9 cm.
 Xem đáp án
Xem đáp án
a)
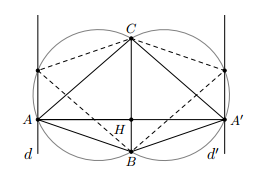
* Cách dựng:
- Dựng đoạn BC = 8 cm.
- Dựng cung chứa góc trên đoạn BC.
- Dựng đường thẳng d song song và cách BC một khoảng bằng 6 cm.
- Đường thẳng d cắt cung chứa góc (ở trên) tại A.
- Nối AB, AC ta được tam giác ABC cần dựng.
* Chứng minh:
Ta có:
- BC = 8 cm (cách dựng)
- vì nằm trên cung chứa góc trên đoạn BC.
- AH = 6 cm vì H nằm trên đường thẳng d song song và cách BC một khoảng bằng 6 cm.
Vậy tam giác ABC thỏa mãn yêu cầu bài toán.
* Biện luận:
Vì d cắt cung chứa góc dựng trên đoạn BC tại hai điểm phân biệt nên bài toán có hai nghiệm hình.
Chú ý: hai tam giác ABC và A’BC (đối xứng nhau qua BC) thỏa mãn yêu cầu đề bài. Do hai tam giác này bằng nhau nên haqi tam giác này chỉ cho ta một nghiệm hình (do đây là bài toán dựng hình về kích thước)
b) Tương tự câu a.
c) Tương tự câu a.
Câu 22:
Dựng tam giác ABC biết
a) BC = 6cm, và trung tuyến AM = 5cm.
b) BC = 4cm, và trung tuyến AM = cm.
 Xem đáp án
Xem đáp án
a)
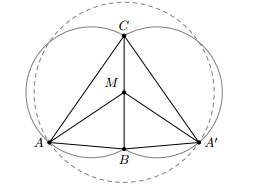
* Cách dựng:
- Dựng đoạn BC = 6 cm và trung điểm M của BC.
- Dựng cung chứa góc trên đoạn BC.
- Dựng đường tròn (M; 5cm) cắt cung chứa góc ở trên tại A.
- Nối AB, AC ta được tam giác ABC.
* Chứng minh:
Ta có: BC = 6cm (cách dựng)
AM = 5 cm (do A nằm trên (M;5cm)
* Biện luận:
Vì (M; 5cm) cắt cung chứa góc dựng trên đoạn BC tại hai điểm phân biệt nên bài toán có hai nghiệm hình.
b) Tương tự câu a.
Câu 23:
Dựng tam giác vuông biết
a) Cạnh huyền bằng 6 cm, bán kính đường tròn nội tiếp bằng 1 cm.
b) Cạnh huyền bằng 5 cm, bán kính đường tròn nội tiếp bằng 1 cm.
 Xem đáp án
Xem đáp án
a)
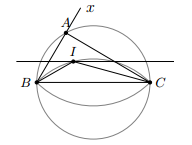
* Cách dựng
- Dựng đoạn BC = 6 cm.
- Dựng cung chứa góc trên đoạn BC.
- Dựng đường thẳng d song song và cách BC một khoảng bằng 1 cm.
- Dựng đường tròn đường kính BC.
- Dựng tia Bx sao cho BI là phân giác góc , khi đó Bx cắt đường tròn đường kính BC tại A.
- Nối AB, AC ta được tam giác ABC.
* Chứng minh:
- Ta có BC = 6 cm (cách dựng)
- (góc nội tiếp chắn nửa đường tròn)
- Khoảng cách từ I đến BC bằng 1 cm (do I nằm trên d). Ta có
Do đó CI là tia phân giác góc
Vậy tam giác ABC thỏa mãn đề bài.
* Biện luận:
Vì d cắt cung chứa góc dựng trên đoạn BC tại hai điểm phân biệt nên bài toán có hai nghiệm hình.
b) Tương tự câu a.
