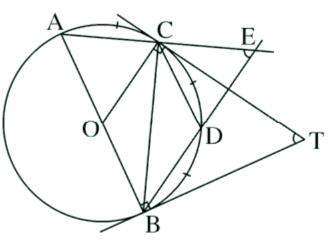
Trên một đường tròn, lấy liên tiếp ba cung AC,CD, DB sao cho
sđ = sđ = sđ
Hai đường thẳng AC và DB cắt nhau tại E. Hai tiếp tuyến của đường tròn tại B và C cắt nhau tại T. Chứng minh rằng:
CD là tia phân giác của
 Giải bởi Vietjack
Giải bởi Vietjack
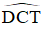
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Qua điểm S nằm bên ngoài đường tròn (O), vẽ tiếp tuyến SA và cát tuyến SBC của đường tròn . Tia phân giác của góc BAC cắt dây BC tại D. Chứng minh SA = SD.
Cho AB và CD là hai đường kính vuông góc của đường tròn (O). Trên cung nhỏ BD lây một điểm M . Tiếp tuyến tại M cắt tia AB ở E, đoạn thẳng CM cắt AB ở S.Chứng minh ES = EM.
Cho đường tròn (O) và hai dây AB, AC. Gọi M, N lần lượt là điểm chính giữa của cung AB và cung AC. Đường thẳng MN cắt dây AB tại E và cắt dây AC tại H. Chứng minh tam giác AEH là tam giác cân.
Qua điểm A nằm bên ngoài đường tròn (O) vẽ hai cát tuyến ABC và AMN sao cho hai đường thẳng BN và CM cắt nhau tại một điểm S nằm bên tròn đường tròn.
Chứng minh
Trên một đường tròn, lấy liên tiếp ba cung AC,CD, DB sao cho
sđ = sđ = sđ
Hai đường thẳng AC và DB cắt nhau tại E. Hai tiếp tuyến của đường tròn tại B và C cắt nhau tại T. Chứng minh rằng:
Cho đường tròn (O) và hai dây cung song song AB, CD (A và C nằm trong cùng một nửa mặt phẳng bờ BD); AD cắt BC tại I. Chứng minh:
Cho tam giác ABC nội tiếp đường tròn. P,Q,R theo thứ tự là các điểm chính giữa của các cung bị chắn BC, CA, AB bởi các góc A, B, C.
Chứng minh AP ⊥ QR.
Cho tam giác ABC nội tiếp đường tròn. P,Q,R theo thứ tự là các điểm chính giữa của các cung bị chắn BC, CA, AB bởi các góc A, B, C.
AP cắt CR tại I. Chứng minh tam giác CPI là tam giác cân.
Hãy chứng minh định lý trên.
Gợi ý: Xem hình 32. Sử dụng góc ngoài của tam giác, chứng minh:
Hãy chứng minh định lí trên
Gợi ý: Sử dụng góc ngoài của tam giác trong ba trường hợp ở hình 36, 37, 38 ( các cung nêu ra dưới hình là những cung bị chắn).