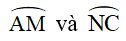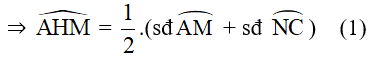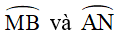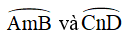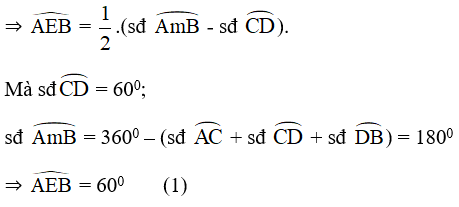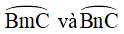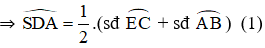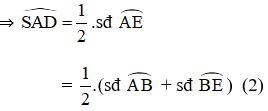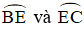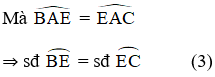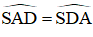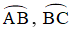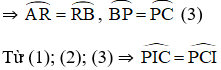Bài 5: Góc có đỉnh ở bên trong đường tròn. Góc có đỉnh ở bên ngoài đường tròn
-
3533 lượt thi
-
11 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 3:
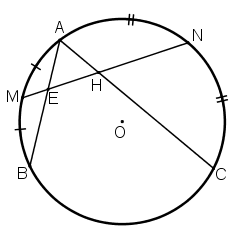
Cho đường tròn (O) và hai dây AB, AC. Gọi M, N lần lượt là điểm chính giữa của cung AB và cung AC. Đường thẳng MN cắt dây AB tại E và cắt dây AC tại H. Chứng minh tam giác AEH là tam giác cân.
 Xem đáp án
Xem đáp án
+ Do góc 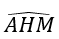
+ Do góc 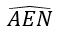
+ Do M và N là điểm chính giữa của cung
Câu 4:
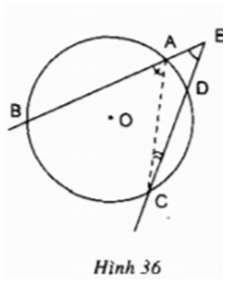
Trên một đường tròn, lấy liên tiếp ba cung AC,CD, DB sao cho
sđ = sđ = sđ
Hai đường thẳng AC và DB cắt nhau tại E. Hai tiếp tuyến của đường tròn tại B và C cắt nhau tại T. Chứng minh rằng:
 Xem đáp án
Xem đáp án
a) + 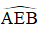
+ 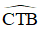
Câu 5:
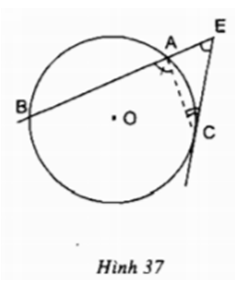
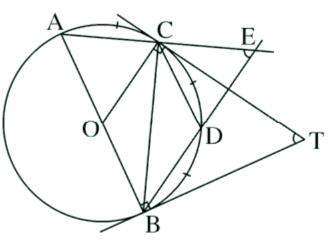
Trên một đường tròn, lấy liên tiếp ba cung AC,CD, DB sao cho
sđ = sđ = sđ
Hai đường thẳng AC và DB cắt nhau tại E. Hai tiếp tuyến của đường tròn tại B và C cắt nhau tại T. Chứng minh rằng:
CD là tia phân giác của
 Xem đáp án
Xem đáp án
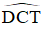
Câu 6:
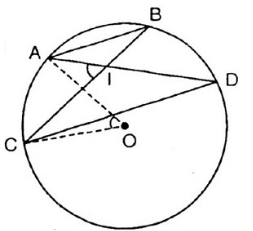
Cho AB và CD là hai đường kính vuông góc của đường tròn (O). Trên cung nhỏ BD lây một điểm M . Tiếp tuyến tại M cắt tia AB ở E, đoạn thẳng CM cắt AB ở S.Chứng minh ES = EM.
 Xem đáp án
Xem đáp án
+ là góc có đỉnh S ở trong đường tròn (O)
+ là góc tạo bởi tiếp tuyến ME và đây MC
Câu 7:
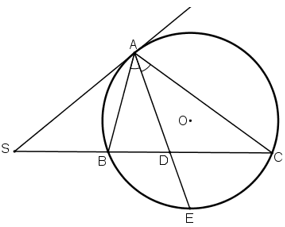
Qua điểm S nằm bên ngoài đường tròn (O), vẽ tiếp tuyến SA và cát tuyến SBC của đường tròn . Tia phân giác của góc BAC cắt dây BC tại D. Chứng minh SA = SD.
 Xem đáp án
Xem đáp án
Tia phân giác AD cắt (O) tại E.
+ 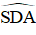
+ 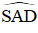
+ 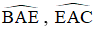
Từ (1); (2) và (3) suy ra
⇒ ΔSAD cân tại S
⇒ SA = SD.
Câu 8:
Qua điểm A nằm bên ngoài đường tròn (O) vẽ hai cát tuyến ABC và AMN sao cho hai đường thẳng BN và CM cắt nhau tại một điểm S nằm bên tròn đường tròn.
Chứng minh
 Xem đáp án
Xem đáp án
(đpcm)
Câu 9:
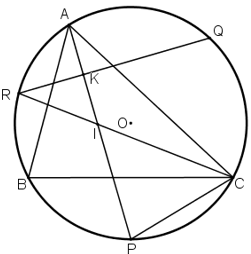
Cho tam giác ABC nội tiếp đường tròn. P,Q,R theo thứ tự là các điểm chính giữa của các cung bị chắn BC, CA, AB bởi các góc A, B, C.
Chứng minh AP ⊥ QR.
 Xem đáp án
Xem đáp án
Gọi K là giao điểm của QR và AP.
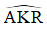
⇒ AP ⊥ QR.
Câu 10:
Cho tam giác ABC nội tiếp đường tròn. P,Q,R theo thứ tự là các điểm chính giữa của các cung bị chắn BC, CA, AB bởi các góc A, B, C.
AP cắt CR tại I. Chứng minh tam giác CPI là tam giác cân.
 Xem đáp án
Xem đáp án
+ R, P lần lượt là điểm chính giữa các cung
⇒ ΔPCI cân tại P.