Cho hình thoi ABCD cạnh a. Gọi R và r lần lượt là bán kính các đường tròn ngoại tiếp tam giác ABD, ABC. Chứng minh rằng: 1R2+1r2=4a2
Giải bởi Vietjack
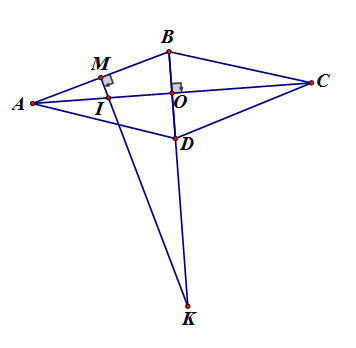
Gọi M, I, K là giao điểm của đường trung trực AB với AB, AC, BD, O là giao điểm của AC và BD.
Ta có: OA=OC,OB=OD,AC⊥BD(Vì ABCD là hình thoi)
Nên AC là trung trực của BD, BD là trung trực của AC
Do đó I, K lần lượt là tâm đường tròn ngoại tiếp ΔADB,ΔABC ⇒IA=R,KB=r
Xét ΔOAB và ΔMKB có ^ABO chung, ^AOB=^KMB(=900)
Do đó: ΔOAB~ΔMKB
⇒OBMB=ABKB⇒OBa2=ar⇒OB2=(a22r)2=a44r2
Tương tự ta có: OA2=a24R2
ΔOAB vuông tại O, theo định lý Pytago ta có:
OA2+OB2=AB2⇒a44R2+a44R2=a2⇒1R2+1r2=4a2(dfcm)
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Cho hình chữ nhật ABCD có AD = 9,3cm, CD = 12,4cm. Chứng minh rằng bốn điểm A, B, C, Dcùng thuộc một đường tròn. Tính bán kính của đường tròn đó.
Cho tam giác ABC nhọn. Vẽ đường tròn (O) có đường kính BC, nó cắt cạnh AB, AC theo thứ tự ở D và E.
a) Chứng minh rằng CD⊥AB,BE⊥AC
b) Gọi K là giao điểm của BE, CD. Chứng minh AK⊥BC
Cho một tứ giác ABCD có 2 đường chéo AC, BD vuông góc với nhau. Gọi M, N, R, S lần lượt là trung điểm các cạnh AB, BC, CD, DA. Chứng minh rằng 4 điểm M, N, R, S cùng nằm trên đường tròn.
Cho hàm số y=f(x)=3x4.
a) Tính f(−1);f(1);f(a)
b) Chứng minh rằng: f(x) = f(-x)