Cho đường tròn (O; R) đường kính AB cố định. Gọi M là trung điểm đoạn OB. Dây CD vuông góc với AB tại M. Điểm E chuyển động trên cung lớn Nối AE cắt CD tại K. Nối BE cắt CD tại H.
a) Chứng minh 4 điểm B, M, E, K thuộc một đường tròn
b) Tính theo R diện tích hình quạt tròn giới hạn bởi OB, OC và cung nhỏ BC.
 Giải bởi Vietjack
Giải bởi Vietjack
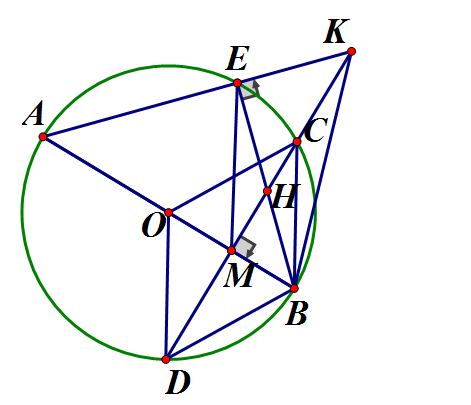
a) Ta có (góc nội tiếp chắn nửa đường tròn)
Tứ giác BMEK có đỉnh M, E liên tiếp cùng nhìn BK dưới 1 góc vuông nên BMEK là tứ giác nội tiếp
cùng thuộc một đường tròn
b) Ta có tại trung điểm M của CD (tính chất đường kính – dây cung)
có hai đường chéo vuông góc tại trung điểm mỗi đường là hình thoi
đều
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Cho tam giác ABC nội tiếp đường tròn (O; 3cm). Tính diện tích hình quạt tròn giới hạn bởi hai bán kính OA, OC và cung nhỏ AC khi
Cho hình vuông có cạnh là 5cm nội tiếp đường tròn (O). Hãy tính chu vi và đường tròn (O) và diện tích hình tròn (O)
Tính diện tích một hình quạt tròn có bán kính 6cm và số đo cung là
Cho đường tròn (O) bán kính R. Vẽ hai đường kính AB, CD của đường tròn (O) vuông góc với nhau. Trên AO lấy E sao cho tia CE cắt đường tròn (O) tại M
a) Chứng minh tứ giác MEOD nội tiếp đường tròn
b) Tính CE theo R
c) Gọi I là giao điểm của CM và AD. Chứng minh
d) Tính diện tích hình tạo bởi dây AD và cung nhỏ AD của đường tròn (O)
Cho a, b, c là ba số thỏa a > b > c > 0 và a + b + c = 12. Chứng minh rằng trong ba phương trình sau :
Có một phương trình có nghiệm, một phương trình vô nghiệm