Một trường tổ chức cho 330 người bao gồm giáo viên và học sinh đi tham quan Dinh Độc Lập. Biết giá vé tham quan tòa nhà chính Di tích lịch sử Dinh Độc Lập của mổi giáo viên là 40 000 đồng, của mỗi học sinh là 20 000 đồng. Nhân dịp kỉ niệm 90 năm Ngày thành lập Đoàn TNCS Hồ Chí Minh (26/3/1931-26/3/2021) nên được giảm 10% cho mỗi vé tham quan, vì vậy mà nhà trường chỉ phải trả số tiền là 6 480 000 đồng. Hỏi có bao nhiêu giáo viên, bao nhiêu học sinh?
 Giải bởi Vietjack
Giải bởi Vietjack
Gọi x là số giáo viên, y là số học sinh (điều kiện: x, y ∈ ℕ, 0 < x, y < 330).
Vì tổng số giáo viên và học sinh đi tham quan là 330 người nên: x + y = 330 (1)
Tổng số tiền vé của giáo viên khi chưa giảm là: 40 000x (đồng).
Tổng số tiền vé của học sinh khi chưa giảm là: 20 000y (đồng).
Tổng số tiền vé của giáo viên và học sinh khi chưa giảm là:
40 000x + 20 000y (đồng).
Mỗi vé tham quan được giảm 10%, tức là giá vé sau khi giảm bằng 90% giá vé ban đầu.
Tổng số tiền vé nhà trường chi trả là 6 480 000 đồng nên ta có phương trình:
90%.(40 000x + 20 000y) = 6 480 000
Û 40 000x + 20 000y = 7 200 000
Û x + 2y = 360 (2)
Từ (1) và (2), ta có hệ phương trình:
Û
Û
Û
Û
Û (thỏa mãn)
Vậy số giáo viên là 30 người và số học sinh là 300 người.
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
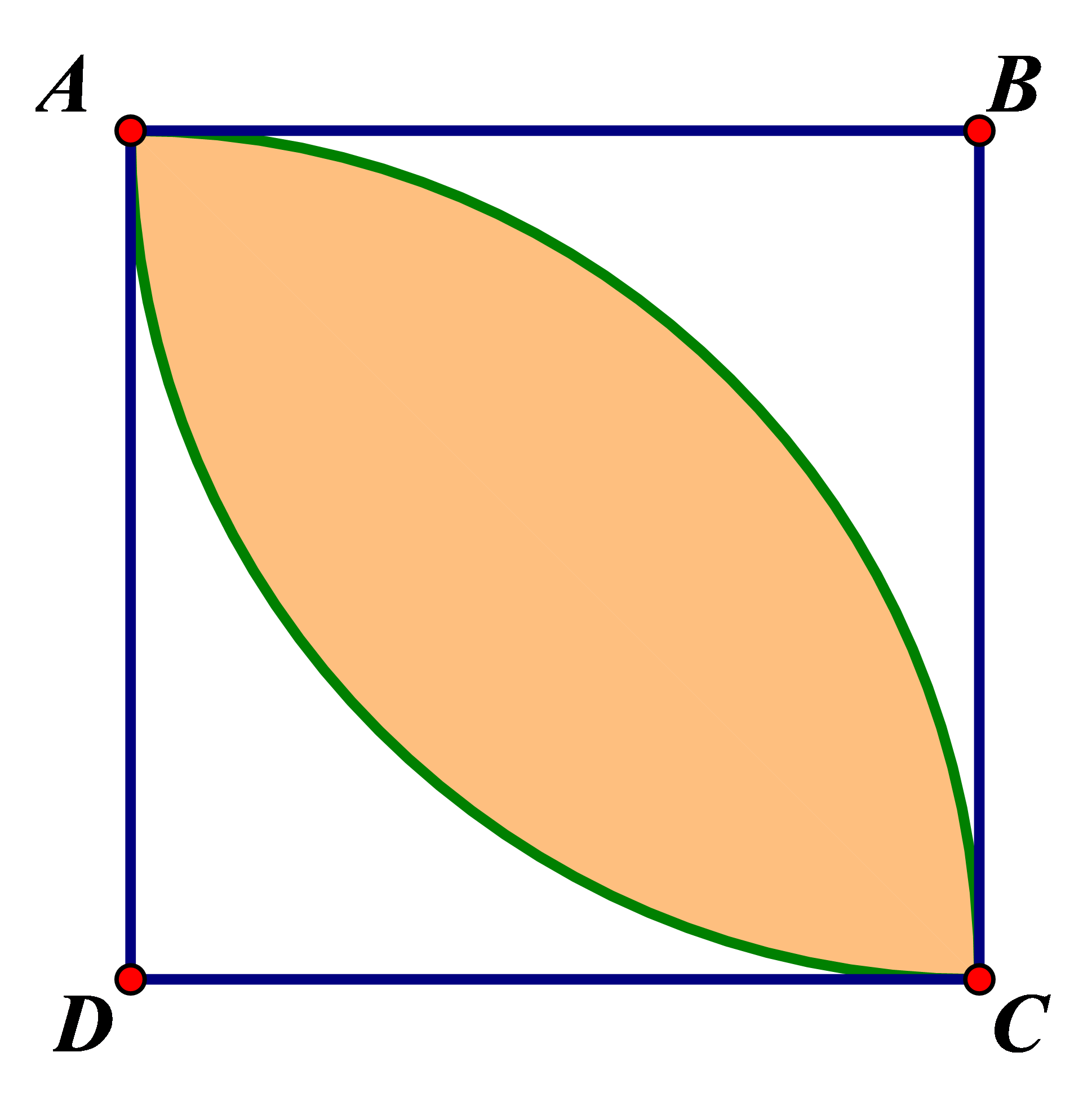
Hoa văn của một tấm bìa hình vuông ABCD cạnh 25cm là hai cung tròn tâm B và tâm D bán kính 25cm có phần chung (phần tô đậm) là hình quả trám như hình vẽ. Hãy tính diện tích phần chung này. (Lấy π ≈ 3,14 và kết quả làm tròn đến chữ số thập phân thứ nhất).
Cho đường tròn (O) và một điểm A nằm ngoài đường tròn (O). Qua điểm A vẽ hai tiếp tuyến AB, AC đến (O) (B, C là 2 tiếp điểm). Gọi H là giao điểm của OA và BC, qua H kẻ một đường thẳng vuông góc với OC cắt (O) tại M (M thuộc cung nhỏ BC), AM cắt (O) tại N (N khác M); gọi K là trung điểm MN.
a) Chứng minh tứ giác ABOC nội tiếp và AB.BM = AM.NB.
b) Chứng minh 5 điểm A, B, K, O, C cùng thuộc 1 đường tròn và .
c) Kẻ OI vuông góc NB tại I. Chứng minh: I, K, H thẳng hàng.
Giải các phương trình sau:
a) 3x2 + 10x + 3 = 0
b) –x4 + 2020x2 + 2021 = 0
c) x3 – 5x2 + 4x = 0
Cho Parabol (P): y = x2 và đường thẳng (d): y = –x + 2.
a) Vẽ (P) trên mặt phẳng tọa độ Oxy.
b) Tìm tọa độ giao điểm của (P) và (d) bằng phép tính.
Cho phương trình 2x2 – mx – 5 = 0 (m là tham số) (1)
a) Chứng tỏ phương trình (1) luôn có 2 nghiệm với mọi m.
b) Gọi x1, x2 là 2 nghiệm của phương trình (1). Tính biểu thức A = x12 – x1 + x22 – x2 theo m.