a) Tính
b) Chứng minh
c) Chứng minh
d) Tính
 Giải bởi Vietjack
Giải bởi Vietjack
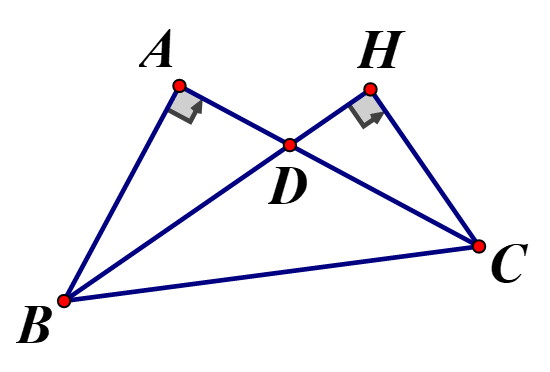
a) BD là tia phân giác nên
b) Do BD là phân giác nên
Và và vuông nên
c) Có (đối đỉnh),
Từ (2) ở câu b ta có:
Từ (2) ở câu b ta có:
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Cho tam giác ABC vuông tại A có . Từ B kẻ tia song song với (Tia Bx thuộc nửa mặt phẳng bờ chứa C), tia phân giác cắt BC tại M và Bxcắt tia tại N
a) Chứng minh
b) Chứng minh
c) Từ N kẻ NE vuông góc với cắt BC tại I. Tính BI
Cho tam giác cân là giao điểm các đường trung trực, D là trung điểm cạnh là trọng tâm của Chứng minh