9 câu hỏi trắc nghiệm thuộc Bài tập theo Tuần toán 8- Tuần 28

Câu 1:

$\begin{array}{l} a) a > b \Leftrightarrow a - 5 > b - 5 \\ b) a > b \Leftrightarrow - a < - b \Leftrightarrow 5 - a < 5 - b \end{array}$

Câu 2:

Cho m>n, CMR:

a) m+3>n+1,

b) 3m+2>3n

Xem đáp án

$\begin{array}{l} a) m > n \Rightarrow m + 3 > n + 3 > n + 1 \Rightarrow m + 3 > n + 1 \\ b) m > n \Leftrightarrow 3 m > 3 n \Leftrightarrow 3 m + 2 > 3 n \end{array}$

Câu 3:

Chứng tỏ rằng với a và b là hai số bất kỳ thì :

$\begin{array}{l} a) a^{2} + b^{2} - 2 a b \geq 0 \\ b) \frac{a^{2} + b^{2}}{2} \geq a b \end{array}$

Xem đáp án

$a) a^{2} + b^{2} - 2 a b \geq 0 \Leftrightarrow {(a - b)}^{2} \geq 0$ ( $l u ô n đ ú n g)$

$b) \frac{a^{2} + b^{2}}{2} \geq a b \Leftrightarrow a^{2} + b^{2} \geq 2 a b \Leftrightarrow a^{2} - 2 a b + b^{2} \geq 0 \Leftrightarrow {(a - b)}^{2} \geq 0$

(luôn đúng) (đpcm)

Câu 4:

Với a,b là các số dương, chứng tỏ : $\frac{a}{b} + \frac{b}{a} \geq 2$

Xem đáp án

$\begin{array}{l} \frac{a}{b} + \frac{b}{a} \geq 2 \Leftrightarrow \frac{a^{2} + b^{2}}{a b} \geq 2 \Leftrightarrow a^{2} + b^{2} \geq 2 a b \Leftrightarrow a^{2} - 2 a b + b^{2} \geq 0 \\ \Leftrightarrow {(a - b)}^{2} \geq 0 (l u o n d u n g) (d f c m) \end{array}$

Câu 5:

Với a bất kỳ, chứng minh $a (a + 2) < {(a + 1)}^{2}$

Xem đáp án

$a (a + 2) < {(a + 1)}^{2} \Leftrightarrow a^{2} + 2 a < a^{2} + 2 a + 1 \Leftrightarrow 0 < 1$

(luôn đúng) (đfcm)

Câu 6:

Cho tam giác ABC vuông tại A có $A B = 6 c m, A C = 8 c m$ . Từ B kẻ tia song song với (Tia Bx thuộc nửa mặt phẳng bờ chứa C), tia phân giác $∠ B A C$ cắt BC tại M và Bxcắt tia tại N

a) Chứng minh $Δ B M N ~ Δ C M A$

b) Chứng minh $A B . A M = A C . M N$

c) Từ N kẻ NE vuông góc với $A C (E \in A C), N E$ cắt BC tại I. Tính BI

Xem đáp án

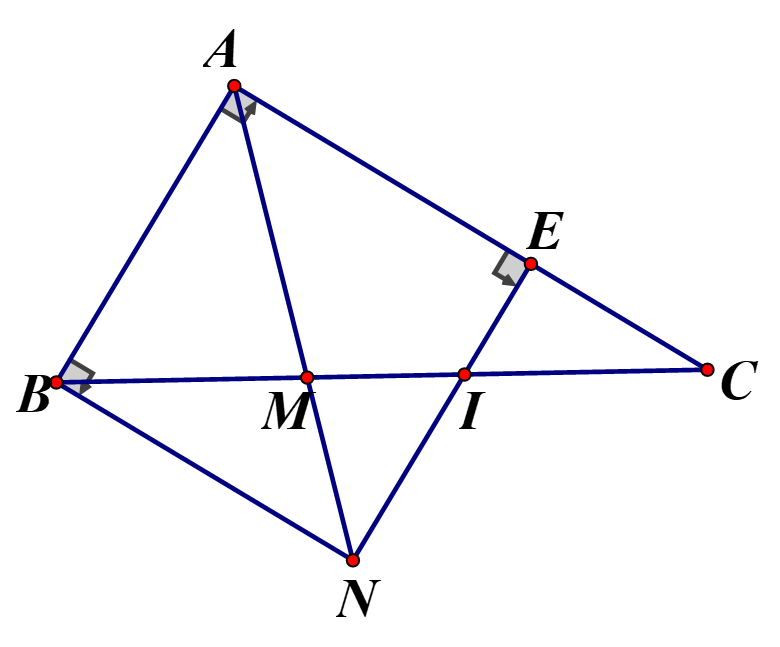
Cho tam giác ABC vuông tại A có AB=6cm, AC=8cm. . Từ B kẻ tia Bx song song với (Tia Bx thuộc nửa mặt phẳng bờ AB chứa C) (ảnh 1)

a) $Δ B M N$ và $Δ C M A$ có : $\hat{N} = \hat{A}$ (so le trong), $\hat{B M N} = \hat{C M A}$ (đối đỉnh)

$\Rightarrow Δ B M N ~ Δ C M A (g - g)$ + $Δ B M N ~ Δ C M A \Rightarrow \frac{B M}{M C} = \frac{M N}{A M} (1)$

b) $\Rightarrow \frac{B M}{M C} = \frac{A B}{A C} (2)$

lại có AM là phân giác

$\frac{M N}{A M} = \frac{A B}{A C} \Rightarrow A B . A M = A C . A N$

Từ (1) và (2) ta có $B C = \sqrt{A B^{2} + A C^{2}} = \sqrt{6^{2} + 8^{2}} = 10 (c m)$

c) Áp dụng định lý Pytago ta có

$\hat{A} = \hat{B} = \hat{E} = 90^{0}$ Tứ giác ABNE có và AN là tia phân giác góc A

$\Rightarrow A E = A B = 6 (c m)$

Nên ABNE là hình vuông

$\Rightarrow C E = A C - A E = 8 - 6 = 2 (c m)$

Ta có $I E / / A B$ (cùng $⊥ A C)$ $\Rightarrow \frac{C I}{C B} = \frac{E C}{A C} h a y \frac{C I}{10} = \frac{2}{6} \Rightarrow C I = \frac{10.2}{6} = \frac{10}{3}$

$\Rightarrow B I = B C - C I = 10 - \frac{10}{3} = \frac{20}{3} (c m)$

Câu 7:

Cho tam giác cân $A B C (A B = A C), O$ là giao điểm các đường trung trực, D là trung điểm cạnh $A B, E$ là trọng tâm của $Δ A C D .$ Chứng minh $O E ⊥ C D$

Xem đáp án

a

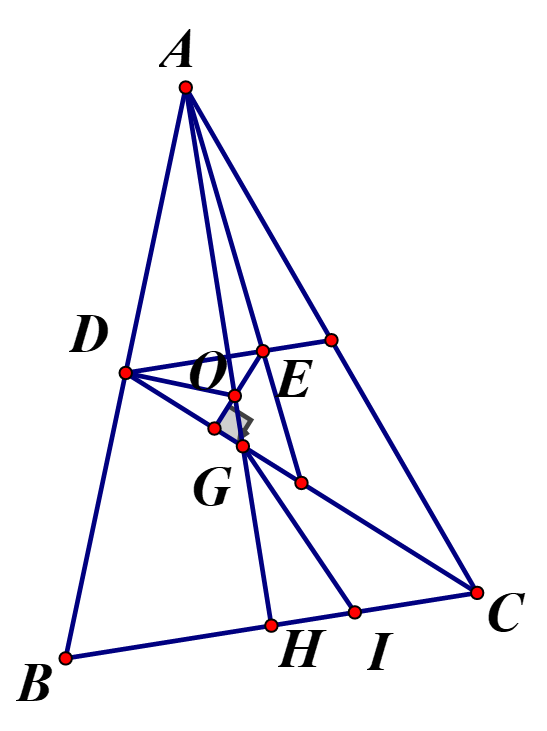
Gọi $H, G$ lần lượt là giao điểm của AO với BC và CD. Lấy $I \in H C$ sao cho $H I = \frac{1}{3} H C$

Do là trọng tâm $Δ A B C$ nên $G H = \frac{1}{3} A H$ .

Vì thế ta có $\frac{H I}{H C} = \frac{H G}{H A} = \frac{1}{3} \Rightarrow G I / / A C \Rightarrow ∠ H G I = ∠ D A O$

$\Rightarrow Δ G H I ~ Δ A D O \Rightarrow \frac{G H}{A D} = \frac{H I}{D O}$

Gọi giao điểm của với là F thì $D E = \frac{2}{3} D F = \frac{2}{3} C H = 2 H I$ mà $A G = 2 G H$

Nên $\frac{A G}{A D} = \frac{D E}{D O}$

Gọi giao điểm của với là thì $D E = \frac{2}{3} D F = \frac{2}{3} C H = 2 H I$ và $A G = 2 G H$ $A G = 2 G H$ nên: $\frac{A G}{A D} = \frac{D E}{D O}$

Lại có $∠ O D E = ∠ D A G$ (hai góc nhọn có cạnh tương ứng vuông góc)

Vì thế : $Δ A D G ~ Δ D O E (c g c)$

Mà $∠ A D O = 90^{0}$ nên góc tạo bởi DG, AO cũng $90^{0} \Rightarrow O E ⊥ C D$

Câu 8:

Cho tam giác ABC vuông tại A có AB=6cm, BC=10cm Tia phân giác Bx của goác ABC cắt AC tại D. Vẽ

C H ⊥ B x (H \in B x)

a) Tính $\frac{D A}{D C}$

b) Chứng minh $Δ A B D ~ Δ H B C$

c) Chứng minh $D A . D C = D B . D H$

d) Tính $D A, D C$

Xem đáp án

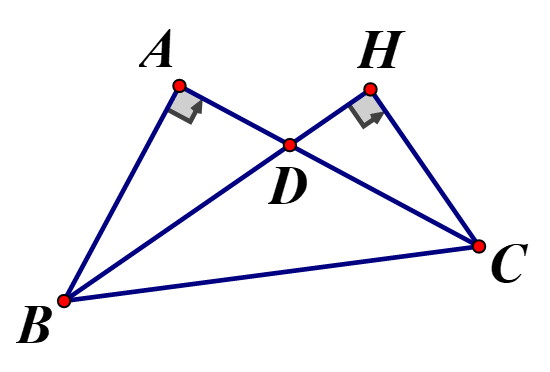
Cho tam giác ABC vuông tại A có AB=6cm, BC=10cm Tia phân giác Bx của goác ABC cắt AC tại D (ảnh 1)

a) BD là tia phân giác $∠ A B C$ nên $\frac{D A}{D C} = \frac{B A}{B C} \Rightarrow \frac{D A}{D C} = \frac{6}{10} = \frac{3}{5}$

b) Do BD là phân giác nên $∠ A B D = ∠ H B C$

Và $Δ A B D$ và $Δ H B C$ vuông nên $Δ A B D = Δ H B C (2)$

c) Có $∠ A D B = ∠ H C D$ (đối đỉnh), $∠ A = ∠ H = 90^{0}$

Từ (2) ở câu b ta có: $\Rightarrow Δ A B D ~ Δ H C D (g . g) \Rightarrow \frac{D A}{D H} = \frac{D B}{D C} \Rightarrow D A . D C = D H . D B$

$\begin{array}{l} \frac{D A}{D C} = \frac{3}{5} \Rightarrow \frac{D A + D C}{D C} = \frac{3 + 5}{5} \Rightarrow \frac{A C}{D C} = \frac{8}{5} \Rightarrow D C = \frac{8.5}{8} = 5 (c m) \\ D A = A C - D C = 8 - 5 = 3 (c m) \Rightarrow S_{A B D} = \frac{A B . A D}{2} = \frac{6.3}{2} = 9 (c m^{2}) \end{array}$

Từ (2) ở câu b ta có: $\begin{array}{l} \frac{S_{A B D}}{S_{H B C}} = \frac{B D^{2}}{B C^{2}} = \frac{A B^{2} + A D^{2}}{B C^{2}} = \frac{6^{2} + 3^{2}}{10^{2}} = \frac{9}{20} \\ \Rightarrow S_{H B C} = \frac{20. S_{A B D}}{9} = \frac{20.9}{9} = 20 (c m^{2}) \end{array}$

Câu 9:

Chứng tỏ rằng với a và b là hai số bất kỳ thì :

\frac{a^{2} + b^{2}}{2} \geq a b

Xem đáp án

$\frac{a^{2} + b^{2}}{2} \geq a b \Leftrightarrow a^{2} + b^{2} \geq 2 a b \Leftrightarrow a^{2} - 2 a b + b^{2} \geq 0 \Leftrightarrow {(a - b)}^{2} \geq 0$

(luôn đúng) (đpcm)

CHỌN BỘ SÁCH BẠN MUỐN XEM

Bài tập cuối tuần Học kì 2 Toán 8 có đáp án

Bài tập theo Tuần toán 8- Tuần 28

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương