Chọn câu đúng:
 Giải bởi Vietjack
Giải bởi Vietjack
Chu vi của một hình bình hành bằng 2 lần tổng một cặp cạnh kề nhau bất kỳ.
Đáp án cần chọn là: D
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Cho hình bình hành có chu vi là 480cm, có độ dài cạnh đáy gấp 5 lần cạnh kia và gấp 8 lần chiều cao. Tính diện tích hình bình hành
Mảnh đất hình bình hành có cạnh đáy là 47 m, mở rộng mảnh đất bằng cách tăng các cạnh đáy của hình bình hành này thêm 7 m thì được mảnh đất hình bình hành mới có diện tích hơn diện tích mảnh đất ban đầu là 189 m2. Hãy tính diện tích mảnh đất ban đầu.
Cho hình bình hành có diện tích là 312 m2, độ dài đáy là 24 m, chiều cao hình bình hành đó là:
Cho khu đất hình bình hành độ dài đáy là 300 dm, chiều cao khu đất hình bình hành là 20 m. Diện tích hình bình hành đó là:
Cho hình bình hành ABCD có chiều cao hạ xuống cạnh CD là 5 cm, chiều dài CD là 15 cm, diện tích hình bình hành ABCD là:
Điền số thích hợp vào ô trống:
Một bình hành có diện tích là 8dm2 và độ dài cạnh đáy là 32cm.
Vậy chiều cao tương ứng với cạnh đáy đó là cm.
Trong các hình dưới đây, hình nào là hình bình hành?
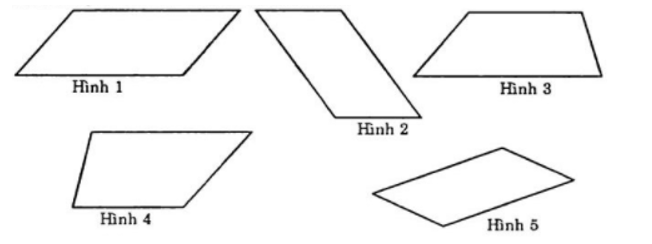
A. Hình 1, hình 2, hình 4
B. Hình 2, hình 3, hình 4
C. Hình 1, hình 4, hình 5
D. Hình 1, hình 2, hình 5
Điền số thích hợp vào ô trống:
Một hình bình hành có diện tích là 1855dm2 và độ dài cạnh đáy là 53dm.
Vậy chiều cao của hình bình hành đó là dm.
Độ dài đáy của hình bình hành có chiều cao 24cm và diện tích là 432cm2 là:
I. Nhận biết Hình bình hành
Cho Hình bình hành | Lý thuyết Toán lớp 6 chi tiết Cánh diều ABCD
Khi đó Hình bình hành | Lý thuyết Toán lớp 6 chi tiết Cánh diều ABCD có:
+ Hai cạnh đối AB và CD, BC và AD song song với nhau;
+ Hai cạnh đối bằng nhau: AB = CD; BC = AD;
+ Hai góc ở các đỉnh A và C bằng nhau; hai góc ở các đỉnh B và D bằng nhau.
II. Vẽ Hình bình hành
Ta có thể vẽ Hình bình hành | Lý thuyết Toán lớp 6 chi tiết Cánh diều bằng thước và compa.
Chẳng hạn, vẽ Hình bình hành | Lý thuyết Toán lớp 6 chi tiết Cánh diều ABCD nhận hai đoạn thẳng AB, AD làm cạnh.
Để vẽ Hình bình hành | Lý thuyết Toán lớp 6 chi tiết Cánh diều ABCD ta thực hiện các bước sau:
Bước 1. Lấy B làm tâm, dùng compa vẽ một phần đường tròn có bán kính AD. Lấy D làm tâm, dùng compa vẽ một phần đường tròn có bán kính AB. Gọi C là giao điểm của hai phần đường tròn này.
Bước 2. Dùng thước vẽ các đoạn thẳng BC và CD.
Ta được Hình bình hành | Lý thuyết Toán lớp 6 chi tiết Cánh diều ABCD.
III. Chu vi và diện tích của Hình bình hành | Lý thuyết Toán lớp 6 chi tiết Cánh diều
Hình bình hành | Lý thuyết Toán lớp 6 chi tiết Cánh diều có độ dài hai cạnh là a và b, độ dài đường cao ứng với cạnh a là h, ta có:
- Chu vi của Hình bình hành | Lý thuyết Toán lớp 6 chi tiết Cánh diều là C = 2(a + b);
- Diện tích của Hình bình hành | Lý thuyết Toán lớp 6 chi tiết Cánh diều là S = a . h.