Tính nhanh: 46 + 17 + 54;

Tính nhanh: 20 + 21 + 22 + ... + 29 + 30

Cho dãy số sau 1, 1, 2, 3, 5, 8, ...

Trong dãy số trên mỗi số (kể từ số thứ ba) bằng tổng của hai số liền trước. Hãy viết tiếp bốn số nữa vào dãy số.

Trên hình 12, đồng hồ chỉ 9 giờ 18 phút, hai kim đồng hồ chia mặt đồng hồ thành hai phần, mỗi phần có sáu số. Tính tổng các số ở mỗi phần, em có nhận xét gì?

Hình 12

Tìm các tích bằng nhau mà không cần tính kết quả của mỗi tích.

15.2.6;     4.4.9;     5.3.12;     8.18;     15.3.4;     8.2.9

Tính nhanh: 463 + 318 + 137 + 22

Tính nhanh: 4.37.25;

Bình Ngô đại cáo ra đời năm nào?

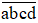
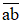
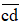
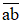
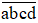
Năm  , Nguyễn Trãi viết Bình Ngô đại cáo tổng kết thắng lợi của cuộc kháng chiến do Lê Lợi lãnh đạo chống quân Minh. Biết rằng  là tổng số ngày trong hai tuần lễ, còn  gấp đôi  . Tính xem năm  là năm nào?

Áp dụng các tính chất của phép cộng và phép nhân để tính nhanh: 86 + 357 + 14

Đố. Số 142857 có tính chất rất đặc biệt. Hãy nhân nó với mỗi số 2, 3, 4, 5, 6 em sẽ tìm được tính chất đăc biệt ấy

Có thể tính nhẩm tích 45.6 bằng cách:

Áp dụng tính chất kết hợp của phép nhân:

45.6 = 45.(2.3) = (45.2).3 = 90 .3 = 270

Áp dụng tính chất phân phối của phép nhân đối với phép cộng:

45.6 = (40+ 5).6 = 40.6 + 5.6 = 240 +30 = 270

Hãy tính nhẩm bằng cách áp dụng tính chất kết hợp của phép nhân:

15.4;         25.12;         125.16

Tính nhanh: 135 + 360 + 65 + 40

Có thể tính nhẩm tích 45.6 bằng cách:

Áp dụng tính chất kết hợp của phép nhân:

45.6 = 45.(2.3) = (45.2).3 = 90 .3 = 270

Áp dụng tính chất phân phối của phép nhân đối với phép cộng:

45.6 = (40+ 5).6 = 40.6 + 5.6 = 240 +30 = 270

Hãy tính nhẩm bằng cách áp dụng tính chất phân phối của phép nhân đối với phép cộng:

25.12;         34.11;         47.101

Cho các số liệu về quãng đường bộ:

      Hà Nội – Vĩnh Yên   : 54km

      Vĩnh Yên – Việt Trì : 19km

      Việt Trì – Yên Bái  : 82km

Tính quãng đường một ô tô đi từ Hà Nội lên Yên Bái qua Vĩnh Yên và Việt Trì.

Tính nhanh: 87.36 + 87.64;

Có thể tính nhanh tổng 97 + 19 bằng cách áp dụng tính chất kết hợp của phép cộng:

97 + 19 = (97 + 3) + 16 = 100 + 16 = 116

Hãy tính nhanh các tổng sau bằng cách làm tương tự như trên: 996 + 45