Cho tứ giác ABCD có BD là phân giác ∠B và BC = CD. Chứng minh tứ giác ABCD là hình thang.
 Giải bởi Vietjack
Giải bởi Vietjack
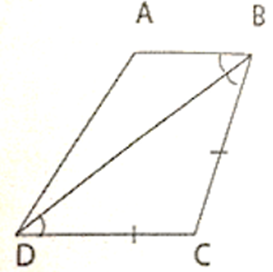
Vì BD là phân giác của ∠ABC
Suy ra ∠ABD = ∠CBD (1)
Lại có BC = CD (gt)
Suy ra ΔCBD cân tại C
Nên ∠CBD = ∠CDB (2)
Từ (1) và (2) suy ra:
∠ABD = ∠CDB Mà 2 góc này ở vị trí so le trong
Suy ra AB // CD
Vậy ABCD là hình thang.
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Hãy điền vào chỗ (…) để được các khẳng định đúng:
Hình thang là tứ giác có ………
Cho tứ giác ABCD. Gọi P, Q, R, S lần lượt là trung điểm của AB, AC, CD, DB.
1. Chứng minh tứ giác PQRS là hình bình hành.
Cho hình thoi ABCD. Gọi O là giao điểm hai đường chéo AC và BD. Đường thẳng qua O không song song với AD cắt AB tại M và CD tại N.
a) Chứng minh ΔAOM = ΔCON.