Trắc nghiệm chuyên đề Toán 8 Chủ đề 13: Ôn tập và kiểm tra có đáp án (Đề 2)
-
819 lượt thi
-
14 câu hỏi
-
50 phút
Danh sách câu hỏi
Câu 2:
Hãy điền vào chỗ (…) để được các khẳng định đúng:
Hình thang là tứ giác có ………
Xem đáp án
Điền: hai cạnh đối song song
Câu 6:
Xem đáp án
Chọn đáp án B
Câu 7:
Xem đáp án
Chọn đáp án C
Câu 9:
Cho hình thoi ABCD. Gọi O là giao điểm hai đường chéo AC và BD. Đường thẳng qua O không song song với AD cắt AB tại M và CD tại N.
a) Chứng minh ΔAOM = ΔCON.
Xem đáp án
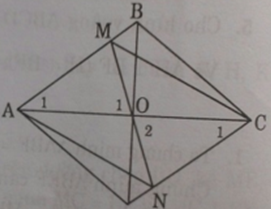
a) Xét ΔAOM và ΔCON có:
∠A1 = ∠C1 (so le trong)
AO = CO (tính chất đường chéo hình thoi)
∠O1 = ∠O1 (đối đỉnh)
Vậy ΔAOM = ΔCON. (c.g.c) ⇒ OM = ON
Câu 10:
b) Chứng tỏ tứ giác AMCN là hình bình hành.
Xem đáp án
b) Xét tứ giác AMCN có OM = ON (cmt), OA = OC (gt)
Do đó AMCN là hình bình hành.
Câu 11:
Cho tứ giác ABCD. Gọi P, Q, R, S lần lượt là trung điểm của AB, AC, CD, DB.
1. Chứng minh tứ giác PQRS là hình bình hành.
Xem đáp án
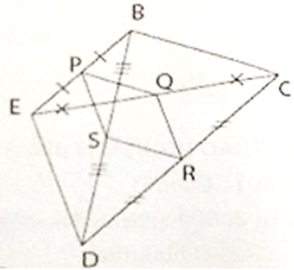
1) Ta có:
• PQ là đường trung bình của ΔABC nên PQ // BC và PQ = (1)
• RS là đường trung bình của ΔDBC nên RS // BC và RS = (2)
Từ (1) và (2) suy ra PQ // RS và PQ = RS
Suy ra tứ giác PQRS là hình bình hành.
Câu 12:
2. Tìm điều kiện của tứ giác ABCD để:
a. PQRS là hình chữ nhật. Xem đáp án
2)
a) Ta có PS là đường trung bình của
Suy ra PS // AD và PS =
Để PQRS là hình chữ nhật ⇔ PQ ⊥ PS ⇔ BC ⊥ AD
Vậy tứ giác ABCD phải thêm điều kiện BC ⊥ AD thì PQRS là hình chữ nhật.
Câu 13:
b. PQRS là hình thoi.
Xem đáp án
b) Để PQRS là hình thoi ⇔ PQ = PS ⇔ BC = AD . Vậy tứ giác ABCD phải thêm điều kiện BC = AD thì PQRS là hình thoi.
Câu 14:
Cho tứ giác ABCD có BD là phân giác ∠B và BC = CD. Chứng minh tứ giác ABCD là hình thang.
Xem đáp án
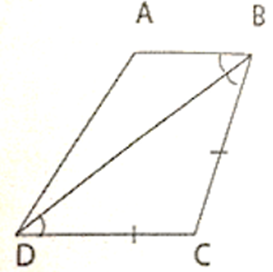
Vì BD là phân giác của ∠ABC
Suy ra ∠ABD = ∠CBD (1)
Lại có BC = CD (gt)
Suy ra ΔCBD cân tại C
Nên ∠CBD = ∠CDB (2)
Từ (1) và (2) suy ra:
∠ABD = ∠CDB Mà 2 góc này ở vị trí so le trong
Suy ra AB // CD
Vậy ABCD là hình thang.