 Giải bởi Vietjack
Giải bởi Vietjack
Hướng dẫn giải:
Gọi tỉ số đồng dạng của Δ A''B''C'' ∼ Δ A'B'C' là k
Ta có:
Điều đố chứng tỏ Δ A''B''C'' ∼ Δ A'B'C' theo tỉ số đồng dạng là k = 1/k1
Gọi tỉ số đồng dạng của Δ A'B'C' ∼ Δ ABC là k3
Thì k1 = A'B'/A''B'' , k2 = A''B''/AB ⇒ k3 = A'B'/AB = A'B'/A''B'' . A''B''/AB = k1 . k2
Điều đó chứng tỏ Δ A'B'C' ∼ Δ ABC theo tỉ số đồng dạng là k3 = k1 k2
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Cho tam giác ABC vuông tại A, đường cao AH có AB = 15cm;AC = 20cm. Tia phân giác của góc HAB cắt HB tại D, tia phân giác của góc HAC cắt HC tại E. Tính độ dài các đoạn AH, HD và HE.
Cho đoạn thẳng AB = 10 cm
a) Trên đoạn thẳng AB lấy điểm C sao cho CA/CB = 3/2 . Tính độ dài đoạn CB.
b) Trên tia đối của tia BA lấy điểm D sao cho DA/DB = 3/2 . Tính độ dài đoạn CD.
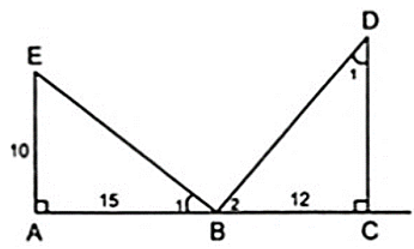
Cho hình vẽ như bên, biết EBAˆ = BDCˆ
a) Trong hình vẽ có bao nhiêu tam giác vuông? Kể tên các tam giác vuông đó.
b) Cho AE = 10cm, AB = 15cm, BC = 12cm. Hãy tính độ dài các đoạn thẳng CD, BE, BD và ED (làm tròn đến chữ số thập phân thứ nhất)
c) So sánh diện tích tam giác BDE với tổng diện tích hai tam giác AEB và BCD
Cho tam giác ABC có BC = a; CA = b; AB = c. Các đường phân giác AD, BE, CF cắt nhau tại I. Chứng minh rằng:
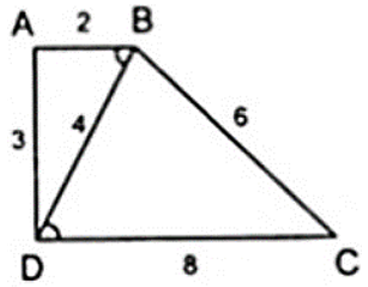
Tứ giác ABCD có AB = 2cm; BC = 6cm; CD = 8cm; DA = 3cm và BD = 4cm. Chứng minh rằng:
a) Δ BAD ∼ Δ DBC
b) ABCD là hình thang
Cho hình thang ABCD ( AB//CD ) có O là giao điểm của hai đường chéo. Đường thẳng qua O song song hai đáy và cắt AD, BC lần lượt tại E và F. Chứng minh OE = OF.
