a) Đọc các số sau: – 9, – 18.
b) Viết các số sau: trừ hai mươi ba; âm ba trăm bốn mươi chín.
 Giải bởi Vietjack
Giải bởi Vietjack
a) Số – 9 được đọc là: "âm chín" hoặc là "trừ chín";
Số – 18 được đọc là: "âm mười tám" hoặc "trừ mười tám".
b) Số "trừ hai mươi ba" được viết là: – 23;
Số "ấm ba trăm bốn mươi chín" được viết là: – 349.
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Bản tin dự báo thời tiết đưới đây cho biết nhiệt độ thấp nhất của một số ngày trong tháng 01/2020 ở Thủ đô Mát-xcơ-va (Moscow, Nga).
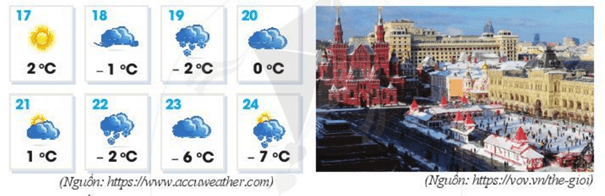
Có những số chỉ nhiệt độ dưới 0 °C như: – 1 °C, – 2 °C, – 6 °C, – 7°C.
Các số trên có gì đặc biệt?
Viết số nguyên âm chỉ năm có các sự kiện sau:
a) Thế vận hội đầu tiên diễn ra năm 776 trước Công nguyên;
b) Nhà toán học Ác-si-mét (Archimedes) sinh năm 287 trước Công nguyên.
Viết số nguyên âm biểu thị độ cao của tàu ngầm so với mực nước biển, biết tàu ngầm đang ở vị trí dưới mực nước biển 20 m.
Viết số nguyên âm biểu thị các tình huống sau:
a) Ông An nợ ngân hàng 4 000 000 đồng;
b) Bà Ba kinh doanh bị lỗ 600 000 đồng.
Bảng thống kê đưới đây cho biết nhiệt độ trong một ngày mùa đông của một vùng xứ lạnh:

a) Đọc và viết nhiệt độ lúc 2 giờ, 10 giờ, 18 giờ, 22 giờ.
b) Xác định tính đúng, sai của các phát biểu sau:
+ Lúc 6 giờ nhiệt độ là – 10 °C;
+ Lúc 14 giờ nhiệt độ là – 3 °C.
Độ sâu lớn nhất của các đại đương dưới mực nước biển
+) Rãnh Ma-ri-a-na (Mariana, thuộc Thái Bình Dương) sâu 10 925 m.

+) Rãnh Pu-éc-tô Ri-cô (Puerto Rico, thuộc Đại Tây Dương) sâu 8 408 m.
+) Rãnh Gia-va (Java, thuộc Ấn Độ Dương) sâu 7 290m.
+) Môn-loi Hâu-lơ (Molloy Hole, nơi sâu nhất của Bắc Băng Dương) sâu 5 669 m.
Hãy sử dụng số nguyên âm để biểu diễn các độ cao đó (so với mực nước biển).



Một hộp có 5 chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số 1, 2, 3, 4, 5; hai thẻ khác nhau thì ghi số khác nhau. Rút ngẫu nhiên một thẻ rồi bỏ lại thẻ vào hộp.
Sau 25 lần rút thẻ liên tiếp, hãy ghi kết quả thống kê theo mẫu sau:
|
Lần 1 |
Số 3 |
Lần 6 |
Số 5 |
Lần 11 |
Số 3 |
Lần 16 |
Số 2 |
Lần 21 |
Số 1 |
|
Lần 2 |
Số 1 |
Lần 7 |
Số 2 |
Lần 12 |
Số 2 |
Lần 17 |
Số 1 |
Lần 22 |
Số 5 |
|
Lần 3 |
Số 2 |
Lần 8 |
Số 3 |
Lần 13 |
Số 2 |
Lần 18 |
Số 2 |
Lần 23 |
Số 3 |
|
Lần 4 |
Số 3 |
Lần 9 |
Số 4 |
Lần 14 |
Số 1 |
Lần 19 |
Số 3 |
Lần 24 |
Số 4 |
|
Lần 5 |
Số 4 |
Lần 10 |
Số 5 |
Lần 15 |
Số 5 |
Lần 20 |
Số 5 |
Lần 25 |
Số 5 |
Tính xác suất thực nghiệm
Xuất hiện số chẵn

Một hộp có 5 chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số 1, 2, 3, 4, 5; hai thẻ khác nhau thì ghi số khác nhau. Rút ngẫu nhiên một thẻ rồi bỏ lại thẻ vào hộp.
Sau 25 lần rút thẻ liên tiếp, hãy ghi kết quả thống kê theo mẫu sau:
|
Lần 1 |
Số 3 |
Lần 6 |
Số 5 |
Lần 11 |
Số 3 |
Lần 16 |
Số 2 |
Lần 21 |
Số 1 |
|
Lần 2 |
Số 1 |
Lần 7 |
Số 2 |
Lần 12 |
Số 2 |
Lần 17 |
Số 1 |
Lần 22 |
Số 5 |
|
Lần 3 |
Số 2 |
Lần 8 |
Số 3 |
Lần 13 |
Số 2 |
Lần 18 |
Số 2 |
Lần 23 |
Số 3 |
|
Lần 4 |
Số 3 |
Lần 9 |
Số 4 |
Lần 14 |
Số 1 |
Lần 19 |
Số 3 |
Lần 24 |
Số 4 |
|
Lần 5 |
Số 4 |
Lần 10 |
Số 5 |
Lần 15 |
Số 5 |
Lần 20 |
Số 5 |
Lần 25 |
Số 5 |
Tính xác suất thực nghiệm
Xuất hiện số 2

Một hộp có 5 chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số 1, 2, 3, 4, 5; hai thẻ khác nhau thì ghi số khác nhau. Rút ngẫu nhiên một thẻ rồi bỏ lại thẻ vào hộp.
Sau 25 lần rút thẻ liên tiếp, hãy ghi kết quả thống kê theo mẫu sau:
|
Lần 1 |
Số 3 |
Lần 6 |
Số 5 |
Lần 11 |
Số 3 |
Lần 16 |
Số 2 |
Lần 21 |
Số 1 |
|
Lần 2 |
Số 1 |
Lần 7 |
Số 2 |
Lần 12 |
Số 2 |
Lần 17 |
Số 1 |
Lần 22 |
Số 5 |
|
Lần 3 |
Số 2 |
Lần 8 |
Số 3 |
Lần 13 |
Số 2 |
Lần 18 |
Số 2 |
Lần 23 |
Số 3 |
|
Lần 4 |
Số 3 |
Lần 9 |
Số 4 |
Lần 14 |
Số 1 |
Lần 19 |
Số 3 |
Lần 24 |
Số 4 |
|
Lần 5 |
Số 4 |
Lần 10 |
Số 5 |
Lần 15 |
Số 5 |
Lần 20 |
Số 5 |
Lần 25 |
Số 5 |
Tính xác suất thực nghiệm
Xuất hiện số 1




