Đường cao của một tam giác vuông chia cạnh huyền thành hai đoạn thẳng có độ dài là 1 và 2. Hãy tính các cạnh góc vuông của tam giác này.
 Giải bởi Vietjack
Giải bởi Vietjack
Lời giải:
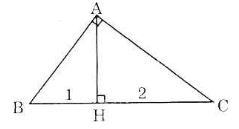
ΔABC vuông tại A và đường cao AH như trên hình.
BC = BH + HC = 1 + 2 = 3
Theo định lí 1: AB2 = BH.BC = 1.3 = 3
=> AB = √3
Theo định lí 1: AC2 = HC.BC = 2.3 = 6
=> AC = √6
Vậy độ dài các cạnh góc vuông của tam giác lần lượt là √3 và √6.
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Cho hình vuông ABCD. Gọi I là một điểm nằm giữa A và B. Tia DI và tia CB cắt nhau ở K. Kẻ đường thẳng qua D, vuông góc với DI. Đường thẳng này cắt đường thẳng BC tại L. Chứng minh rằng:
a) Tam giác DIL là một tam giác cân.
b) Tổng không đổi khi I thay đổi trên cạnh AB.
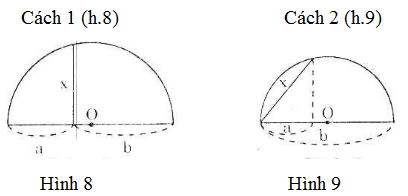
Người ta đưa ra hai cách vẽ đoạn trung bình nhân x của hai đoạn thẳng a, b (tức là x2 = ab) như trong hai hình sau:
Dựa vào các hệ thức (1) và (2), hãy chứng minh các cách vẽ trên là đúng.
Gợi ý: Nếu một tam giác có đường trung tuyến ứng với một cạnh bằng nữa cạnh đó thì tam giác ấy là tam giác vuông.
Trong tam giác vuông với các cạnh góc vuông có độ dài 3 và 4, kẻ đường cao ứng với cạnh huyền. Hãy tính đường cao này và độ dài các đoạn thẳng mà nó định ra trên cạnh huyền.