Công ty Ánh Dương có lợi nhuận ở mỗi tháng trong Quý I là – 30 triệu đồng. Trong Quý II, lợi nhuận mỗi tháng của công ty là 70 triệu đồng. Sau 6 tháng đầu năm, lợi nhuận của công ty Ánh Dương là bao nhiêu tiền?

Tính 8. 25. Từ đó suy ra kết quả của các phép tính sau:

a) (– 8) . 25;

b) 8 . (– 25);

c) (– 8) . (– 25).

Sử dụng máy tính cầm tay

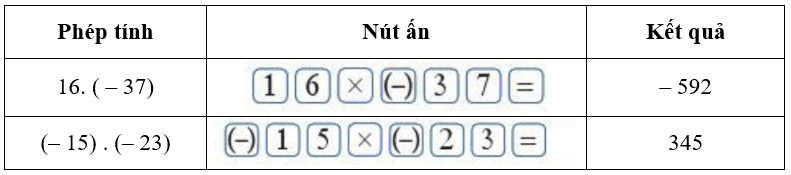
Dùng máy tính cầm tay để tính:

23 . (– 49); 

(– 215) . 207; 

(– 124) . (– 1 023).

Chọn từ “âm”, “dương” thích hợp cho (?)

a) Tích ba số nguyên âm là một số nguyên (?);

b) Tích hai số nguyên âm với một số nguyên dương là một số nguyên (?);

c) Tích của một số chẵn các số nguyên âm là một số nguyên (?);

d) Tích của một số lẻ các số nguyên âm là một số nguyên (?).

Tính một cách hợp lí:

a) (– 6) . (– 3) . (– 5);

b) 41 . 81 – 41. (– 19).

Tính:

a) ${10}^{10}$ . (– ${10}^4$), 

b) (– 2) . (– 2) . (– 2) . (– 2) . (– 2) + $2^5$;

c) (– 3) . (– 3) . (– 3) . (– 3) – $3^4$.

Tính giá trị của biểu thức trong mỗi trường hợp sau:

a) 2x, biết x = – 8; 

b) – 7y, biết y = 6; 

c) – 8z – 15, biết z = – 4.

Tính và so sánh kết quả:

a) (– 4) . 7 và 7 . (– 4); 

b) [(– 3). 4] . (– 5) và (– 3) . [4. (– 5)];

c) (– 4) . 1 và – 4; 

d) (– 4) . (7 + 3) và (– 4) . 7 + (– 4) . 3.

a) Hoàn thành phép tính: (– 3) . 4 = (– 3) + (– 3) + (– 3) + (– 3) = (?).

b) So sánh (– 3). 4 và – (3. 4).

Tính một cách hợp lí:

a) (– 16) . (– 7) . 5; 

b) 11. (– 12) + 11. (– 18);

c) 87. (– 19) – 37 . (– 19); 

d) 41 . 81 .(– 451). 0.

Tính giá trị của biểu thức trong mỗi trường hợp sau:

a) – 6x – 12 với x = – 2;

b) – 4y + 20 với y = – 8.

Tính:

a) 21 . (– 3); 

b) (– 16) . 5; 

c) 12 . 20; 

d) (– 21) . (– 6).

Tìm số thích hợp ở (?):

a) Quan sát kết quả của ba tích đầu, ở đó mỗi lần ta giảm 1 đơn vị ở thừa số thứ hai. Tìm kết quả của hai tích cuối.

(– 3) . 2 = – 6

(– 3) . 1 = – 3 tăng 3 đơn vị

(– 3) . 0 = 0 tăng 3 đơn vị

(– 3) . (–1) = (?1) tăng 3 đơn vị

(– 3) . (– 2) = (?2) tăng 3 đơn vị

b) So sánh (– 3). (– 2) và 3. 2.

Tính:

a) (– 7) . 5;

b) 11 . (– 13).

Ta đã biết 3 . 2 = 6. Phải chăng (– 3) . (– 2) = – 6?